【题目】先化简,再求值:
(1)(x+1)2+x(x-2),其中x=-![]() ;
;
(2)[(xy+2)(xy-2)-2(x2y2-2)]÷xy,其中x=10,y=-![]() ;
;
(3)已知a+b=12,ab=20,求a(a+b)(a-b)-a(a+b)2的值.
参考答案:
【答案】(1)![]() ; (2)
; (2) ![]() ; (3)-480.
; (3)-480.
【解析】
(1)先去括号,再合并同类项,然后代入数据求解即可;
(2)根据平方差公式和单项式乘多项式计算,再利用单项式的除法计算化简,然后代入数据求解即可;
(3)先提取公因式化简,再用整体代入法求解即可.
(1)原式=x2+2x+1+x2-2x=2x2+1.
当x=-![]() 时,原式=2×(﹣
时,原式=2×(﹣![]() )2+1=
)2+1=![]() ;
;
(2)原式=(x2y2-4-2x2y2+4)÷xy
=(-x2y2)÷xy=-xy,
当x=10,y=-![]() 时,原式=-10×(﹣
时,原式=-10×(﹣![]() )=
)=![]() ;
;
(3)原式=a(a+b)[a-b-(a+b)]=a(a+b)·(-2b)
=-2ab(a+b)=-2×20×12=-480.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.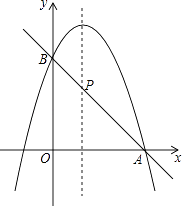
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为  m.
m. 
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米? -
科目: 来源: 题型:
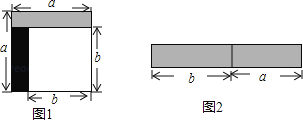
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2 B、a2﹣b2=(a+b)(a﹣b) C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下题:
计算:(1﹣
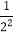 )(1﹣
)(1﹣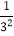 )(1﹣
)(1﹣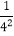 )…(1﹣
)…(1﹣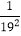 )(1﹣
)(1﹣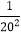 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )

A.110°
B.80°
C.40°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.
其中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形两边x、y的长满足|x2﹣4|+
 =0,则第三边长为 .
=0,则第三边长为 .
相关试题

