【题目】解方程: ![]() .
.
参考答案:
【答案】解:方程的两边同乘(x﹣1)(x+1),得
3x+3﹣x﹣3=0,
解得x=0.
检验:把x=0代入(x﹣1)(x+1)=﹣1≠0.
∴原方程的解为:x=0
【解析】观察可得最简公分母是(x﹣1)(x+1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.本题考查了分式方程和不等式组的解法,注:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.(3)不等式组的解集的四种解法:大大取大,小小取小,大小小大中间找,大大小小找不到.
【考点精析】根据题目的已知条件,利用去分母法的相关知识可以得到问题的答案,需要掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=
 CD,求证:∠AEF=90°.
CD,求证:∠AEF=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3tan30°﹣
 +(2016+π)0+(﹣
+(2016+π)0+(﹣  )﹣2 .
)﹣2 . -
科目: 来源: 题型:
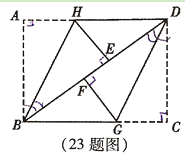
查看答案和解析>>【题目】(10分) 把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0个﹣2,;乙袋中有3个完全相同的小球,分别标有数字﹣2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y)
(1)写出先Q所有可能的坐标;
(2)求点Q在x轴上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD的对角线BD上的一点,且BE=BC,AB=3,BC=4,点P为直线EC上的一点,且PQ⊥BC于点Q,PR⊥BD于点R.

(1)①如图1,当点P为线段EC中点时,易证:PR+PQ=
 (不需证明).②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(不需证明).②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(2)如图3,当点P为线段EC延长线上的任意一点时,其它条件不变,则PR与PQ之间又具有怎样的数量关系?请直接写出你的猜想.
相关试题

