【题目】如图,点E是矩形ABCD的对角线BD上的一点,且BE=BC,AB=3,BC=4,点P为直线EC上的一点,且PQ⊥BC于点Q,PR⊥BD于点R.

(1)①如图1,当点P为线段EC中点时,易证:PR+PQ= ![]() (不需证明).②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(不需证明).②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(2)如图3,当点P为线段EC延长线上的任意一点时,其它条件不变,则PR与PQ之间又具有怎样的数量关系?请直接写出你的猜想.
参考答案:
【答案】(1)成立,理由见解析;(2)PR﹣PQ=![]()
【解析】
试题(1)②连接BP,过C点作CK⊥BD于点K.根据矩形的性质及勾股定理求出BD的长,根据三角形面积相等可求出CK的长,最后通过等量代换即可证明;
(2)图3中的结论是PR﹣PQ=![]() .
.
试题解析:解:(1)②图2中结论PR+PQ=![]() 仍成立.
仍成立.
证明:连接BP,过C点作CK⊥BD于点K.
∵四边形ABCD为矩形,∴∠BCD=90°.又∵CD=AB=3,BC=4,∴BD=![]() =
=![]() =5.
=5.
∵S△BCD=![]() BCCD=
BCCD=![]() BDCK,∴3×4=5CK,∴CK=
BDCK,∴3×4=5CK,∴CK=![]() .
.
∵S△BCE=![]() BECK,S△BEP=
BECK,S△BEP=![]() PRBE,S△BCP=
PRBE,S△BCP=![]() PQBC,且S△BCE=S△BEP+S△BCP,∴
PQBC,且S△BCE=S△BEP+S△BCP,∴![]() BECK=
BECK=![]() PRBE+
PRBE+![]() PQBC.又∵BE=BC,∴
PQBC.又∵BE=BC,∴![]() CK=
CK=![]() PR+
PR+![]() PQ,∴CK=PR+PQ.又∵CK=
PQ,∴CK=PR+PQ.又∵CK=![]() ,∴PR+PQ=
,∴PR+PQ=![]() ;
;
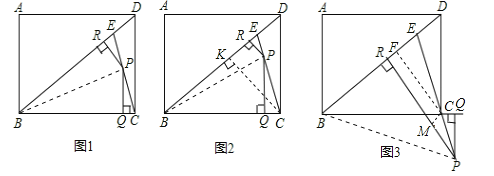
(2)过C作CF⊥BD交BD于F,作CM⊥PR交PR于M,连接BP,S△BPE﹣S△BCP=S△BEC,S△BEC是固定值,BE=BC为两个底,PR,PQ 分别为高,图3中的结论是PR﹣PQ=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
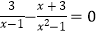 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0个﹣2,;乙袋中有3个完全相同的小球,分别标有数字﹣2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y)
(1)写出先Q所有可能的坐标;
(2)求点Q在x轴上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( )

A. 17 B. 18 C. 19 D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.

(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】
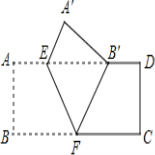
A.12 B. 24 C. 12
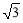 D. 16
D. 16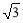
相关试题

