【题目】我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)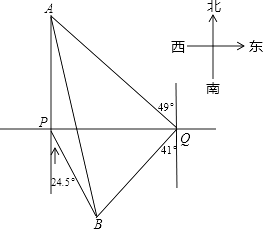
参考答案:
【答案】解:∵∠PQB=90°﹣41°=49°,
∠BPQ=90°﹣24.5°=65.5°,
∴∠PBQ=180°﹣49°﹣65.5°=65.5°,
∴∠BPQ=∠PBQ,
∴BQ=PQ;
∵∠AQB=180°﹣49°﹣41°=90°,∠PQA=90°﹣49°=41°,
∴AQ= ![]() =
= ![]() =1600,
=1600,
∵BQ=PQ=1200,
∴AB2=AQ2+BQ2=16002+12002,
∴AB=2000,
答:A、B的距离为2000m
【解析】首先由已知求出∠PBQ和∠BPQ的度数得出线段BQ与PQ,根据已知求出∠PQA,再由直角三角形PQA求出AQ,又由已知得∠AQB=90°,所以根据勾股定理求出A,B间的距离.
【考点精析】通过灵活运用关于方向角问题,掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕
 )的值;
)的值;(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若这个方程有一个根为﹣2,求k的值和方程的另一个根. -
科目: 来源: 题型:
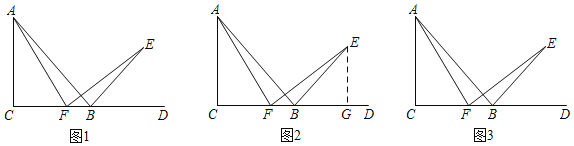
查看答案和解析>>【题目】数学课上,老师给出了如下问题:
已知:如图1,在Rt△ABC中,∠C=90°,AC=BC,延长CB到点D,∠DBE=45°,点F是边BC上一点,连结AF,作FE⊥AF,交BE于点E.
(1)求证:∠CAF=∠DFE;
(2)求证:AF=EF.
经过独立思考后,老师让同学们小组交流.小辉同学说出了对于第二问的想法:“我想通过构造含有边AF和EF的全等三角形,因此我过点E作EG⊥CD于G(如图2所示),如果能证明Rt△ACF和Rt△FGE全等,问题就解决了.但是这两个三角形证不出来相等的边,好像这样作辅助线行不通.”小亮同学说:“既然这样作辅助线证不出来,再考虑有没有其他添加辅助线的方法.”请你顺着小亮同学的思路在图3中继续尝试,并完成(1)、(2)问的证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是一个无理数筛选器的工作流程图.
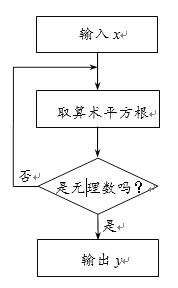
(1)当
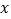 为16时,
为16时,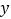 值为 ;
值为 ;(2)是否存在输入有意义的
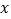 值后,却始终输不出
值后,却始终输不出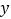 值?如果存在,写出所有满足要求的
值?如果存在,写出所有满足要求的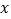 值;如果不存在,请说明理由;
值;如果不存在,请说明理由;(3)如果输入
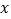 值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的
值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的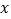 值可能是什么情况;
值可能是什么情况;(4)当输出的
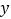 值是
值是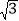 时,判断输入的
时,判断输入的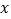 值是否唯一,如果不唯一,请写出其中的两个.
值是否唯一,如果不唯一,请写出其中的两个. -
科目: 来源: 题型:
查看答案和解析>>【题目】顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:
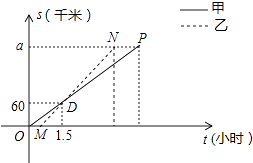
(1)分别计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A地?并在图中画出甲、乙两车在返回过程中离A地的距离S(km)与时间t(h)的函数图象.
相关试题

