【题目】数学课上,老师给出了如下问题:
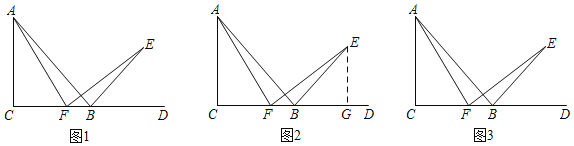
已知:如图1,在Rt△ABC中,∠C=90°,AC=BC,延长CB到点D,∠DBE=45°,点F是边BC上一点,连结AF,作FE⊥AF,交BE于点E.
(1)求证:∠CAF=∠DFE;
(2)求证:AF=EF.
经过独立思考后,老师让同学们小组交流.小辉同学说出了对于第二问的想法:“我想通过构造含有边AF和EF的全等三角形,因此我过点E作EG⊥CD于G(如图2所示),如果能证明Rt△ACF和Rt△FGE全等,问题就解决了.但是这两个三角形证不出来相等的边,好像这样作辅助线行不通.”小亮同学说:“既然这样作辅助线证不出来,再考虑有没有其他添加辅助线的方法.”请你顺着小亮同学的思路在图3中继续尝试,并完成(1)、(2)问的证明.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)依据“同角的余角相等”,即可得到∠CAF=∠DFE;
(2)在AC 上截取AG=BF,连结FG,依据ASA即可判定△AGF≌△FBE,进而得出AF=EF.
证明:(1)∵∠C=90°,
∴∠CAF+∠AFC=90°.
∵FE⊥AF,
∴∠DFE+∠AFC=90°.
∴∠CAF=∠DFE.
(2)如图3,在AC上截取AG=BF,连结FG,
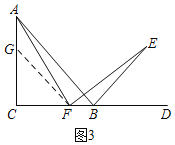
∵AC=BC,
∴AC-AG=BC-BF,即CG=CF.
∵∠C=90°,
∴∠CGF=∠CFG=45°.
∴∠AGF=180°-∠CGF=135°.
∵∠DBE=45°,
∴∠FBE=180°-∠DBE=135°.
∴∠AGF=∠FBE.
由(1)可得:∠CAF=∠DFE.
∴△AGF≌△FBE(ASA).
∴AF=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年8月1日是中国人民解放军成立90周年纪念日,某学校团委为此准备举行“学唱红歌”歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱曲目,为此提供代号为A,B,C,D四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制如下两幅不完整的统计图.请根据图①、图②所提供的信息,解答下列问题:

(1)本次抽样调查的学生有名,其中选择曲目代号为A的学生所对应圆心角的度数为;
(2)请将图②补充完整;
(3)若该校共有1800名学生,根据抽样调查的结果估计全校共有多少名学生选择代号为C的曲目为必唱歌曲? -
科目: 来源: 题型:
查看答案和解析>>【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕
 )的值;
)的值;(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若这个方程有一个根为﹣2,求k的值和方程的另一个根. -
科目: 来源: 题型:
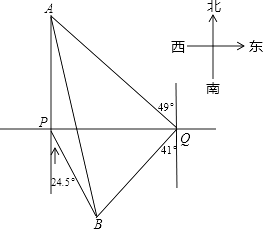
查看答案和解析>>【题目】我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是一个无理数筛选器的工作流程图.
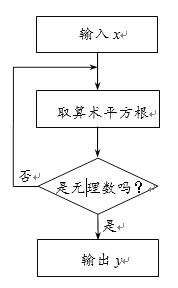
(1)当
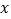 为16时,
为16时,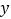 值为 ;
值为 ;(2)是否存在输入有意义的
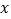 值后,却始终输不出
值后,却始终输不出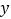 值?如果存在,写出所有满足要求的
值?如果存在,写出所有满足要求的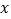 值;如果不存在,请说明理由;
值;如果不存在,请说明理由;(3)如果输入
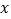 值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的
值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的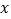 值可能是什么情况;
值可能是什么情况;(4)当输出的
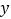 值是
值是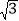 时,判断输入的
时,判断输入的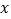 值是否唯一,如果不唯一,请写出其中的两个.
值是否唯一,如果不唯一,请写出其中的两个.
相关试题

