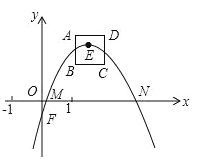
【题目】如图,抛物线l:y=﹣x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
(1)直接写出点D的坐标_____________;
(2)若l经过点B,C,求l的解析式;
(3)设l与x轴交于点M,N,当l的顶点E与点D重合时,求线段MN的值;当顶点E在正方形ABCD内或边上时,直接写出线段MN的取值范围;
(4)若l经过正方形ABCD的两个顶点,直接写出所有符合条件的c的值.
参考答案:
【答案】(1)D点的坐标为(2,2);(2)y=﹣x2+3x﹣1;(3)2≤MN≤![]() ;(4)所有符合条件的c的值为﹣1,1,﹣2.
;(4)所有符合条件的c的值为﹣1,1,﹣2.
【解析】试题分析:(1)根据正方形的性质,可得D点的坐标;
(2)根据待定系数法,可得函数解析式;
(3)根据顶点横坐标纵坐标越大,与x轴交点的线段越长,根据顶点横坐标纵坐标越小,与x轴交点的线段越短,可得答案;
(4)根据待定系数法,可得c的值,要分类讨论,以防遗漏.
试题解析:解:(1)由正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1),得D点的横坐标等于C点的横坐标,即D点的横坐标为2,D点的纵坐标等于A点的纵坐标,即D点的纵坐标为2,D点的坐标为(2,2);
(2)把B(1,1)、C(2,1)代入解析式可得:![]() ,解得:
,解得:![]()
所以二次函数的解析式为y=﹣x2+3x﹣1;
(3)由此时顶点E的坐标为(2,2),得:抛物线解析式为y=﹣(x﹣2)2+2
把y=0代入得:﹣(x﹣2)2+2=0
解得:x1=2﹣![]() ,x2=2+
,x2=2+![]() ,即N(2+
,即N(2+![]() ,0),M(2﹣
,0),M(2﹣![]() ,0),所以MN=2+
,0),所以MN=2+![]() ﹣(2﹣
﹣(2﹣![]() )=2
)=2![]() .
.
点E的坐标为B(1,1),得:抛物线解析式为y=﹣(x﹣1)2+1
把y=0代入得:﹣(x﹣1)2+1=0
解得:x1=0,x2=2,即N(2,0),M(0,0),所以MN=2﹣0=2.
点E在线段AD上时,MN最大,点E在线段BC上时,MN最小;
当顶点E在正方形ABCD内或边上时,2≤MN≤2![]() ;
;
(4)当l经过点B,C时,二次函数的解析式为y=﹣x2+3x﹣1,c=﹣1;
当l经过点A、D时,E点不在正方形ABCD内或边上,故排除;
当l经过点B、D时,![]() ,解得:
,解得:![]() ,即c=﹣2;
,即c=﹣2;
当l经过点A、C时,![]() ,解得
,解得![]() ,即c=1;
,即c=1;
综上所述:l经过正方形ABCD的两个顶点,所有符合条件的c的值为﹣1,1,﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上第一行的数是1,第二行的数是13,第三行的数是43,…,依此规律,第五行的数是( )
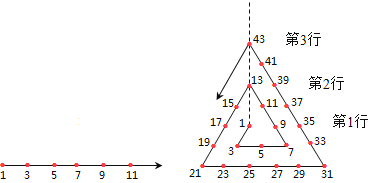
A. 183 B. 157 C. 133 D. 91
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店试销一款成本为 50 元的排球,规定试销期间单价不低于成本价,且获利不得高于 40%。经试销发现,销售量
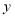 (个)与销售单价
(个)与销售单价 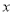 (元)之间满足如图所示的一次函数关系.
(元)之间满足如图所示的一次函数关系.(1)试确定
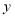 与
与 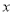 之间的函数关系式;
之间的函数关系式;(2)若该体育用品商店试销的这款排球所获得的利润为
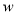 元,试写出利润
元,试写出利润 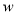 (元)与销售单价
(元)与销售单价 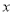 (元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?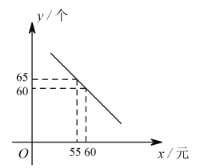
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,AC=BC,∠A=30°,点D在AB边上且∠ADC=45°.
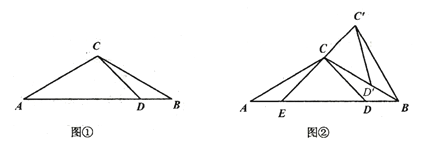
(1)求∠BCD的度数;
(2)将图①中的△BCD绕点B顺时针旋转,得到△BC′D′.当点D′恰好落在BC边上时,如图②所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°).
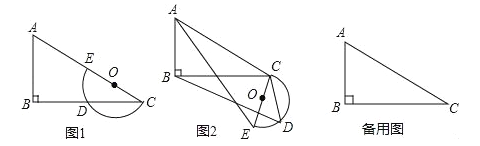
(1)当α=0°时,连接DE,则∠CDE= °,CD= ;
(2)试判断:旋转过程中
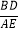 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;(3)若m=10,n=8,当旋转的角度α恰为∠ACB的大小时,求线段BD的长;
(4)若m=6,n=
 ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.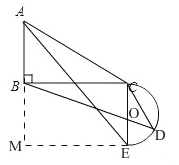
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一根绳子对折成一条线段AB,在线段AB取一点P,使AP=
 ,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm.
,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm. -
科目: 来源: 题型:
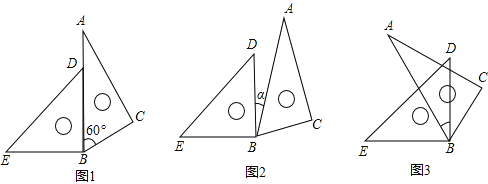
查看答案和解析>>【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.
相关试题

