【题目】如图,△ACB和△ECD都是等腰直角三角形,△ACB的锐角顶点A在△ECD的斜边DE上,若AE=![]() ,AC=
,AC=![]() ,则DE=____.
,则DE=____.
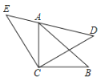
参考答案:
【答案】![]() .
.
【解析】
连结BD,由等腰直角三角形的性质得出∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,由SAS证明△AEC≌△BDC,得出AE=BD,证出∠BDA=∠BDC+∠ADC=90°,在Rt△ADB中.由勾股定理求得AD,即可得出结论.
解:连结BD,如图,
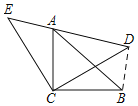
∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,
∵∠ECD-∠ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD,
在△AEC和△BDC中,
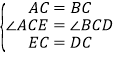 ,
,
∴△AEC≌△BDC(SAS).
∴AE=BD=![]() ,∠E=∠BDC=45°,
,∠E=∠BDC=45°,
∴∠BDA=∠BDC+∠ADC=90°,
在Rt△ACB中.AB=![]() AC=
AC=![]() ,
,
由勾股定理得:AD= ![]() =
=![]() =
=![]() ,
,
∴DE=AE+AD=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
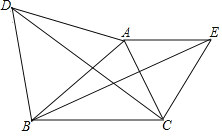
查看答案和解析>>【题目】如图,已知△ABC ,分别以AB 、AC 为边在△ABC 的外部作等边三角形ABD和等边三角形ACE联结DC 、BE 试说明DCBE的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,已知△ ABC 中,点 D 、E 是 BC 边上两点,且 ADAE ,BAECAD 90 ,
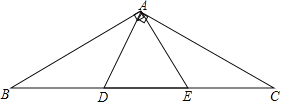
(1)试说明△ABE 与△ACD 全等的理由;
(2)如果 ADBD ,试判断△ADE 的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,在平面直角坐标系中,直线AB∥ x轴,线段AB与 y 轴交于点M ,已知点 A的坐标是(-2,3), BM4,点C 与点 B 关于 x 轴对称.

(1)在图中描出点C ,并直接写出点 B 和点C 的坐标:B ,C ;
(2)联结 AC 、BC ,AC 与 x 轴交于点 D ,试判断△ABC 的形状,并直接写出点 D的坐标;
(3)在坐标平面内, x 轴的下方,是否存在这样的点 P ,使得△ACP 是等腰直角三角形?如果存在,直接写出点P 的坐标;如果不存在,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(3分)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD∶GC∶EB的结果(不必写计算过程);
(2)(3分)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD∶GC∶EB;
(3)(2分)把图(2)中的正方形都换成矩形,如图(3),且已知DA∶AB=HA∶AE=m: n,此时HD∶GC∶EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).

-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=
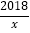 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】整顿药品市场、降低药品价格是国家的惠民政策之一.根据国家《药品政府定价办法》,某省有关部门规定:市场流通药品的零售价格不得超过进价的15%.根据相关信息解决下列问题:
(1)降价前,甲乙两种药品每盒的出厂价格之和为6.6元.经过若干中间环节,甲种药品每盒的零售价格比出厂价格的5倍少2.2元,乙种药品每盒的零售价格是出厂价格的6倍,两种药品每盒的零售价格之和为33.8元.那么降价前甲、乙两种药品每盒的零售价格分别是多少元?
(2)降价后,某药品经销商将上述的甲、乙两种药品分别以每盒8元和5元的价格销售给医院,医院根据实际情况决定:对甲种药品每盒加价15%、对乙种药品每盒加价10%后零售给患者.实际进药时,这两种药品均以每10盒为1箱进行包装.近期该医院准备从经销商处购进甲乙两种药品共100箱,其中乙种药品不少于40箱,销售这批药品的总利润不低于900元.请问购进时有哪几种搭配方案?
相关试题

