【题目】如图 ,已知△ ABC 中,点 D 、E 是 BC 边上两点,且 ADAE ,BAECAD 90 ,
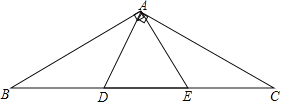
(1)试说明△ABE 与△ACD 全等的理由;
(2)如果 ADBD ,试判断△ADE 的形状,并说明理由.
参考答案:
【答案】(1)见解析;(2)△ ADE 是等边三角形.理由见解析.
【解析】
(1)由ADAE得到AED ADE,再由BAECAD 90 即可得到△ABE ≌△ACD;
(2) 由AD BD 得到BAD B,依据三角形内角和求得AED 60 可得到△ADE是等边三角形.
(1)∵ AD AE (已知),
∴AED ADE (等边对等角).
在△ABE 和△ACD 中
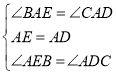 ,
,
∴△ABE ≌△ACD(ASA);
(2)△ADE是等边三角形.
理由:∵AD BD ,
∴BAD B(等边对等角).
设B 的度数为 x ,则BAD 的度数为 x .
∵ADE B BAD( 三角形的一个外角等于与它不相邻的两个内角的和),
∴ADE AED 2x .
∵B AEB BAE 180(三角形的内角和等于 180°),
∴ x 2x 90 180,
解得 x 30 ,
∴AED 60 .
∵AD AE(已知),
∴△ADE 是等边三角形(有一个内角等于 60°的等腰三角形是等边三角形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1=


图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1,再过点C1作C1C2⊥BC于点C2,又过点C2作C2C3⊥AB于点C3,如此无限继续下去,则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形
 中,
中, ,则添加下列条件,不能使四边形
,则添加下列条件,不能使四边形 成为平行四边形的是( )
成为平行四边形的是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC ,分别以AB 、AC 为边在△ABC 的外部作等边三角形ABD和等边三角形ACE联结DC 、BE 试说明DCBE的理由.
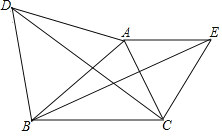
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,在平面直角坐标系中,直线AB∥ x轴,线段AB与 y 轴交于点M ,已知点 A的坐标是(-2,3), BM4,点C 与点 B 关于 x 轴对称.

(1)在图中描出点C ,并直接写出点 B 和点C 的坐标:B ,C ;
(2)联结 AC 、BC ,AC 与 x 轴交于点 D ,试判断△ABC 的形状,并直接写出点 D的坐标;
(3)在坐标平面内, x 轴的下方,是否存在这样的点 P ,使得△ACP 是等腰直角三角形?如果存在,直接写出点P 的坐标;如果不存在,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,△ACB的锐角顶点A在△ECD的斜边DE上,若AE=
 ,AC=
,AC=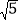 ,则DE=____.
,则DE=____.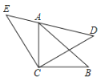
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(3分)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD∶GC∶EB的结果(不必写计算过程);
(2)(3分)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD∶GC∶EB;
(3)(2分)把图(2)中的正方形都换成矩形,如图(3),且已知DA∶AB=HA∶AE=m: n,此时HD∶GC∶EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).

相关试题

