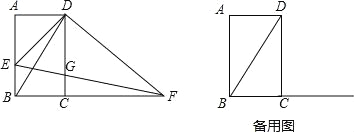
【题目】如图,在矩形ABCD中,BC=1,∠CBD=60°,点E是AB边上一动点(不与点A,B重合),连接DE,过点D作DF⊥DE交BC的延长线于点F,连接EF交CD于点G.
(1)求证:△ADE∽△CDF;
(2)求∠DEF的度数;
(3)设BE的长为x,△BEF的面积为y.
①求y关于x的函数关系式,并求出当x为何值时,y有最大值;
②当y为最大值时,连接BG,请判断此时四边形BGDE的形状,并说明理由.
参考答案:
【答案】(1)证明见解析;
(2)∠DEF=60°;
(3)①y=﹣(x﹣![]() )2+
)2+![]() ,
,
∴当x为![]() 时,y有最大值;
时,y有最大值;
②四边形BGDE是平行四边形.
【解析】试题分析:(1)根据平行四边形的性质得到∠A=∠ADC=∠DCB=90°,根据余角的性质得到∠ADE=∠CDF,由相似三角形的判定定理即可得到结论;
(2)解直角三角形得到CD=![]() ,根据矩形的性质得到AD=BC=1.AB=CD=
,根据矩形的性质得到AD=BC=1.AB=CD=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() =
=![]() ,根据三角函数的定义即可得到结论;
,根据三角函数的定义即可得到结论;
(3)①根据相似三角形的性质得到CF=3﹣![]() x,根据三角形的面积公式得到函数的解析式,根据二次函数的顶点坐标即可得到结论;②根据当x为
x,根据三角形的面积公式得到函数的解析式,根据二次函数的顶点坐标即可得到结论;②根据当x为![]() 时,y有最大值,得到BE=
时,y有最大值,得到BE=![]() ,CF=1,BF=2,根据相似三角形的想得到CG=
,CF=1,BF=2,根据相似三角形的想得到CG=![]() ,于是得到BE=DG,由于BE∥DG,即可得到结论.
,于是得到BE=DG,由于BE∥DG,即可得到结论.
试题解析:(1)在矩形ABCD中,
∵∠A=∠ADC=∠DCB=90°,
∴∠A=∠DCF=90°,
∵DF⊥DE,
∴∠A=∠EDF=90°,
∴∠ADE=∠CDF,
∴△ADE∽△CDF;
(2)∵BC=1,∠DBC=60°,
∴CD=![]() ,
,
在矩形ABCD中,
∵AD=BC=1.AB=CD=![]() ,
,
∵△ADE∽△CDF,
∴![]() ,
,
∵tan∠DEF=![]() ,
,
∴![]() =
=![]() ,
,
∴∠DEF=60°;
(3)①∵BE=x,
∴AE=![]() ﹣x,
﹣x,
∵△ADE∽△CDF,
∴![]() ,
,
∴CF=3﹣![]() x,
x,
∴BF=BC+CF=4﹣![]() x,
x,
∴y=![]() BEBF=
BEBF=![]() x(4﹣
x(4﹣![]() x)=﹣
x)=﹣![]() x2+2x,
x2+2x,
∵y=﹣![]() x2+2x=﹣(x﹣
x2+2x=﹣(x﹣![]() )2+
)2+![]() ,
,
∴当x为![]() 时,y有最大值;
时,y有最大值;
②y为最大值时,此时四边形BGDE是平行四边形,
∵当x为![]() 时,y有最大值,
时,y有最大值,
∴BE=![]() ,CF=1,BF=2,
,CF=1,BF=2,
∵CG∥BE,
∴△CFG∽△BFE,
∴![]() ,
,
∴CG=![]() ,
,
∴DG=![]() ,
,
∴BE=DG,∵BE∥DG,
∴四边形BGDE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b的图象与反比例函数y=
 的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<﹣1).
的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<﹣1).(1)求反比例函数的解析式;
(2)用含t的式子表示k,b;
(3)若△AOB的面积为3,求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.a2+a3=a5
B.a3a4=a12
C.a6÷a3=a2
D.4a﹣a=3a -
科目: 来源: 题型:
查看答案和解析>>【题目】六十四名学生外出参加竞赛,共租车10辆,其中大车每辆可坐8人,小车每辆可坐4人,则大、小车各租多少辆?
-
科目: 来源: 题型:
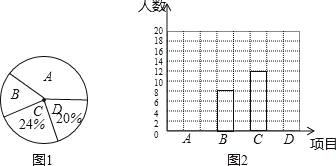
查看答案和解析>>【题目】某校开展阳光体育活动,要求每名学生从以下球类活动中选择一项参加体育锻炼:A﹣乒乓球;B﹣足球;C﹣篮球;D﹣羽毛球.学校王老师对八年级某班同学的活动选择情况进行调查统计,绘制了两幅不完整的统计图,如图所示.
(1)请你求出该班学生的人数并补全条形统计图;
(2)已知该校八年级学生共有500人,学校根据统计调查结果进行预估,按参加项目人数每10人购买一个训练用球的标准,为B,C两个项目统一购买训练用球.经了解,某商场销售的足球比篮球的单价少30元,此时学校共需花费2700元购买足球和篮球.求该商场销售的足球和篮球的单价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
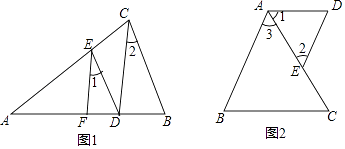
(1)如图,已知,∠AEF=∠ACD,∠1=∠2,求证:DE∥BC.(要求:不写根据)
(2)∠1=∠C,∠B=∠D,求证:∠3=∠2.(要求:不写根据;不许用三角形的内角和定理) -
科目: 来源: 题型:
查看答案和解析>>【题目】若x=3是方程x2﹣3mx+6m=0的一个根,则m的值为( )
A.1
B.2
C.3
D.4
相关试题

