【题目】如图,△ABC和△ADE中,AB=AD,BC=DE,∠B=∠D,边AD与边BC交于点P(不与点B、C重合),点B、E在AD异侧,I为△APC的内心(三条角平线的交点) .

(1)求证:∠BAD=∠CAE;
(2)当∠BAC=90°时,
①若AB=16,BC=20时,求线段PD的最大值;
②若∠B=36°,∠AIC的取值范围为m°<∠AIC<n°,求m、n的值.
参考答案:
【答案】(1)见解析;(2)①![]() ;②
;②![]() ,
,![]()
【解析】
(1)运用已知条件,依据SAS可证![]() ,从而可得
,从而可得![]() ,减去重合部分,即得所求证;
,减去重合部分,即得所求证;
(2)①![]() ,
,![]() ,当
,当![]() 时,
时,![]() 最小,
最小,![]() =最大,运用等面积法求出
=最大,运用等面积法求出![]() ,即可得出结论;
,即可得出结论;
②用三角形内角和定理求出![]() ,运用内心,求出
,运用内心,求出![]() ,设
,设![]() ,则
,则![]() 可用α表示,根据三角形内角和定理,∠AIC也可用α表示,由于
可用α表示,根据三角形内角和定理,∠AIC也可用α表示,由于![]() ,所以∠AIC的取值范围也能求出来.
,所以∠AIC的取值范围也能求出来.
(1)证明:![]() 在
在![]() 与
与![]() 中
中
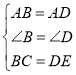 ,
,
![]() (SAS)
(SAS)
![]()
![]()
即![]()
(2)①![]() 中,
中,![]() ,
,
由勾股定理,得![]()
![]() ,而
,而![]() .
.
![]() 当
当![]() 时,
时,![]() 最小,
最小,![]() 最大,
最大,
此时,![]() ,即
,即![]() ,
,
解得![]() ,
,
![]() 的最大值
的最大值![]()
②如图,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
![]() 为
为![]() 的内心,
的内心,
![]() 、
、![]() 分别平分
分别平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
又![]() ,
,![]() ,
,
即![]() ,
,
![]() ,
,![]() .
.
-
科目: 来源: 题型:
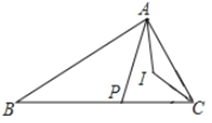
查看答案和解析>>【题目】如果一个三角形的所有顶点都在网格的格点上,那么这个三角形叫做格点三角形,请在下列给定网格中按要求解答下面问题:
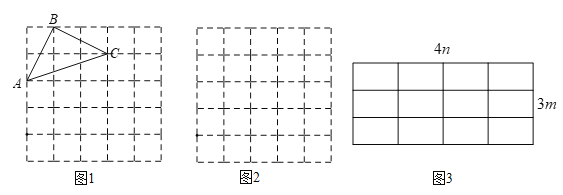
(1)直接写出图1方格图(每个小方格边长均为1)中格点△ABC的面积;
(2)已知△A1B1C1三边长分别为
 、
、 、
、 ,在图2方格图(每个小方格边长均为1)中画出格点△A1B1C1;
,在图2方格图(每个小方格边长均为1)中画出格点△A1B1C1;(3)已知△A2B2C2三边长分别为
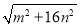 、
、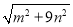 、
、  (m>0,n>0,且m≠n)在图3所示4n×3m网格中画出格点△A2B2C2,并求其面积.
(m>0,n>0,且m≠n)在图3所示4n×3m网格中画出格点△A2B2C2,并求其面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】参加学校运动会,八年级1班第一天购买了水果,面包,饮料,药品等四种食品,四种食品购买金额的统计图表如图1、图2所示,若将水果、面包、药品三种食品统称为非饮料食品,并规定t=饮料金额:非饮料金额.

(1)①求t的值;
②求扇形统计图中钝角∠AOB的度数
(2)根据实际需要,该班第二天购买这四种食品时,增加购买饮料金额,同时减少购买面包金额假设增加购买饮料金额的25%等于减少购买面包的金额,且购买面包的金额不少于100元,求t的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为a,射线AM是∠A外角的平分线,点E在边AB上运动(不与点A、B重合),点F在射线AM上,且AF=√2BE,CF与AD相交于点G,连结EC、EF、EG.
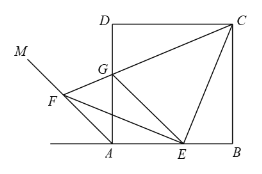
(1)求证:CE=EF;
(2)求△AEG的周长(用含a的代数式表示)
(3)试探索:点E在边AB上运动至什么位置时,△EAF的面积最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
,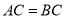 ,直线
,直线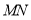 经过点
经过点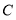 ,且
,且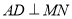 于点
于点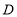 ,
,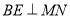 于点
于点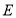 .
.
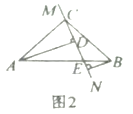
(1)当直线
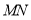 绕点
绕点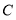 旋转到图1的位置时,求证:
旋转到图1的位置时,求证:①
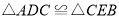 ;
;②
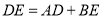 .
.(2)当直线
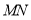 绕点
绕点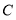 旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由.
旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
相关试题

