【题目】在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.

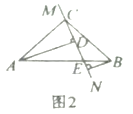
(1)当直线![]() 绕点
绕点![]() 旋转到图1的位置时,求证:
旋转到图1的位置时,求证:
①![]() ;
;
②![]() .
.
(2)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由.
旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由.
参考答案:
【答案】(1)①见解析,②见解析;(2)不成立,理由见解析.
【解析】
(1)①由条件可证明△ADC≌△CEB(AAS);②利用全等三角形的性质和线段的和差可证得结论;
(2)同(1)可证得△ACD≌△CBE,利用全等三角形的性质可求得DE=AD-BE即可解答.
解:(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠DCA=∠DCA+∠BCE=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
∠ADC=∠BEC,
∠DAC=∠ECB,
AC=BC,
∴△ADC≌△CEB(AAS);
②∴△ADC≌△CEB
∴AD=CE,CD=BE,
∵DE=CD+CE,
∴DE=AD+BE;
(2)不成立,理由如下,
由(1)可得,同理可证△ADC≌△CEB,
∴CD=BE,AD=CE,
∵DE=CE-CD,
∴DE=AD-BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】参加学校运动会,八年级1班第一天购买了水果,面包,饮料,药品等四种食品,四种食品购买金额的统计图表如图1、图2所示,若将水果、面包、药品三种食品统称为非饮料食品,并规定t=饮料金额:非饮料金额.

(1)①求t的值;
②求扇形统计图中钝角∠AOB的度数
(2)根据实际需要,该班第二天购买这四种食品时,增加购买饮料金额,同时减少购买面包金额假设增加购买饮料金额的25%等于减少购买面包的金额,且购买面包的金额不少于100元,求t的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE中,AB=AD,BC=DE,∠B=∠D,边AD与边BC交于点P(不与点B、C重合),点B、E在AD异侧,I为△APC的内心(三条角平线的交点) .

(1)求证:∠BAD=∠CAE;
(2)当∠BAC=90°时,
①若AB=16,BC=20时,求线段PD的最大值;
②若∠B=36°,∠AIC的取值范围为m°<∠AIC<n°,求m、n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为a,射线AM是∠A外角的平分线,点E在边AB上运动(不与点A、B重合),点F在射线AM上,且AF=√2BE,CF与AD相交于点G,连结EC、EF、EG.
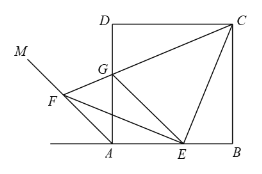
(1)求证:CE=EF;
(2)求△AEG的周长(用含a的代数式表示)
(3)试探索:点E在边AB上运动至什么位置时,△EAF的面积最大?
-
科目: 来源: 题型:
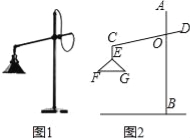
查看答案和解析>>【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
-
科目: 来源: 题型:
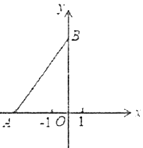
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
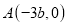 ,为
,为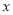 轴负半轴上一点,点
轴负半轴上一点,点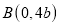 为
为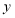 轴正半轴上一点,其中
轴正半轴上一点,其中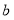 满足方程
满足方程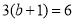 .
.
(1)求点
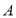 、
、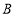 的坐标;
的坐标;(2)点
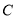 为
为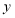 轴负半轴上一点,且
轴负半轴上一点,且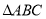 的面积为
的面积为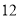 ,求点
,求点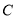 的坐标;
的坐标;(3)在
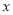 上是否存在一点
上是否存在一点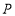 ,使
,使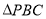 的面积等于
的面积等于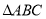 的面积的一半,若存在,求出相应的
的面积的一半,若存在,求出相应的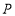 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,地面上小山的两侧有
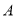 ,
,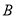 两地,为了测量
两地,为了测量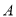 ,
,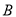 两地的距离,让一热气球从小山西侧
两地的距离,让一热气球从小山西侧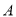 地出发沿与
地出发沿与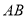 成
成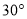 角的方向,以每分钟
角的方向,以每分钟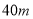 的速度直线飞行,
的速度直线飞行,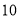 分钟后到达
分钟后到达 处,此时热气球上的人测得
处,此时热气球上的人测得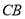 与
与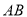 成
成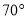 角,请你用测得的数据求
角,请你用测得的数据求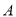 ,
,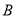 两地的距离
两地的距离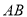 长.(结果用含非特殊角的三角函数和根式表示即可)
长.(结果用含非特殊角的三角函数和根式表示即可)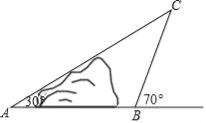
相关试题

