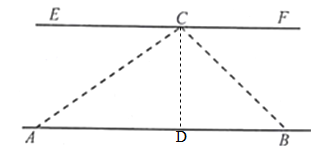
【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)

参考答案:
【答案】湛河的宽度约60米
【解析】试题分析:过C作CD⊥AB于点D,设CD=x米.由∠CBD=45°,得到BD=CD=x .
在Rt△ADC中,用tan∠CAD表示出AD .根据AB=AD+DB=140,列方程求解即可.
试题解析:解:过C作CD⊥AB于点D,设CD=x米.
在Rt△BDC中,∠CDB=90°,∠CBD=45°,∴BD=CD=x .
在Rt△ADC中,∠ADC=90°,∠CAD=37°,∴AD=![]() .
.
∵AB=AD+DB=140,∴![]() ,∴x=60.
,∴x=60.
答:湛河的宽度约60米.
-
科目: 来源: 题型:
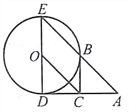
查看答案和解析>>【题目】如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于点B,且四边形BCOE是平行四边形。
(1)BC是⊙O的切线吗?若是,给出证明:若不是,请说明理由;
(2)若⊙O半径为1,求AD的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A,B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,当P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于
 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )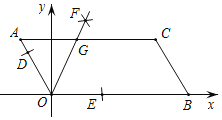
A. (
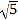 ﹣1,2) B. (
﹣1,2) B. (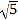 ,2) C. (3﹣
,2) C. (3﹣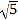 ,2) D. (
,2) D. (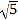 ﹣2,2)
﹣2,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(
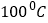 ),王红家只有刻度不超过
),王红家只有刻度不超过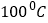 的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔
的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔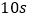 测量一次锅中油温,测量得到的数据如下表:
测量一次锅中油温,测量得到的数据如下表:时间
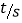
0
10
20
30
40
油温
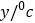
10
30
50
70
90
王红发现,烧了
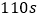 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )A. 没有加热时,油的温度是
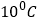
B. 加热
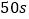 ,油的温度是
,油的温度是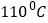
C. 估计这种食用油的沸点温度约是
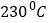
D. 每加热
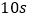 ,油的温度升高
,油的温度升高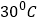
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=6,△BCD为等边三角形,点E为△BCD围成的区域(包括各边)内的一点,过点E作EM∥AB,交直线AC于点M,作EN∥AC,交直线AB于点N,则
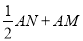 的最大值为_____.
的最大值为_____.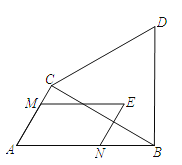
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车行经销的
 型自行车去年
型自行车去年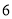 月份销售总额为
月份销售总额为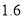 万元,今年由于改造升级每辆车售价比去年增加
万元,今年由于改造升级每辆车售价比去年增加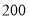 元,今年
元,今年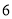 月份与去年同期相比,销售数量相同,销售总额增加
月份与去年同期相比,销售数量相同,销售总额增加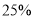 .
.(1)求今年
 型车每辆售价多少元?
型车每辆售价多少元?(2)该车行计划
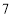 月份用不超过
月份用不超过 万元的资金新进一批
万元的资金新进一批 型车和
型车和 型车共
型车共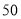 辆,应如何进货才能使这批车售完后获利最多?
辆,应如何进货才能使这批车售完后获利最多?今年
 、
、 两种型号车的进价和售价如下表:
两种型号车的进价和售价如下表: 型车
型车 型车
型车进价(元/辆)
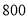
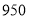
售价(元/辆)
今年售价
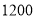
相关试题

