【题目】如图:已知A(0,-2),B(-2,1),C(3,2)
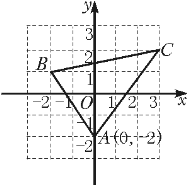
(1)求线段AB、BC、AC的长;
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求A′B′、B′C′、A′C′的长;
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
参考答案:
【答案】(1)![]() ,
,![]() ,AC=5;(2)A′B′
,AC=5;(2)A′B′![]() ,B′C′=
,B′C′=![]() ,A′C′=10;(3)成比例;(4)相同.
,A′C′=10;(3)成比例;(4)相同.
【解析】
试题分析:(1)根据勾股定理结合格点的特征即可求得结果;
(2)根据勾股定理结合格点的特征即可求得结果;
(3)由![]() 即可判断;
即可判断;
(4)根据两个三角形的三组对边对应成比例即可判断.
(1)AB=![]() ,BC=
,BC=![]() ,AC=
,AC=![]() =5
=5
(2)由已知得A′(0,-4),B′(-4,2),C′(6,4)
则A′B′=![]() ,B′C′=
,B′C′=![]() ,A′C′=
,A′C′=![]() =10;
=10;
(3)∵![]()
∴这六条线段成比例;
(4)△ABC与△A′B′C′的形状相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
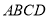 中,对角线
中,对角线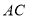 与
与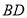 交于点
交于点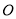 .过点
.过点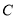 作
作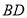 的平行线,过点
的平行线,过点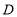 作
作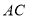 的平行线,两直线相交于点
的平行线,两直线相交于点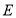 .
.(1)求证:四边形
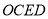 是矩形;
是矩形;(2)若
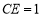 ,
,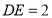 ,则菱形
,则菱形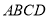 的面积是 .
的面积是 .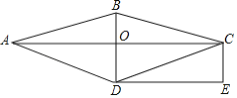
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=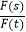 ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间的距离为300(
 +1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
+1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
相关试题

