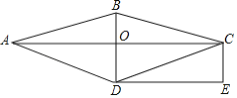
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() .过点
.过点![]() 作
作![]() 的平行线,过点
的平行线,过点![]() 作
作![]() 的平行线,两直线相交于点
的平行线,两直线相交于点![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,
,![]() ,则菱形
,则菱形![]() 的面积是 .
的面积是 .
参考答案:
【答案】(1)证明见解析;(2)4.
【解析】
(1)欲证明四边形OCED是矩形,只需推知四边形OCED是平行四边形,且有一内角为90度即可;
(2)由菱形的对角线互相垂直平分和菱形的面积公式解答.
(1)证明:∵四边形ABCD是菱形,

∴AC⊥BD,
∴∠COD=90°.
∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形,
又∠COD=90°,
∴平行四边形OCED是矩形;
(2)由(1)知,平行四边形OCED是矩形,则CE=OD=1,DE=OC=2.
∵四边形ABCD是菱形,
∴AC=2OC=4,BD=2OD=2,
∴菱形ABCD的面积为:![]() ACBD=
ACBD=![]() ×4×2=4.
×4×2=4.
故答案是:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
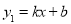 与
与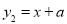 图象如图所示,则下列结论:①
图象如图所示,则下列结论:①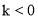 ;②
;②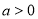 ;③关于
;③关于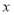 的方程
的方程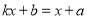 的解为
的解为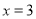 ;④当
;④当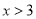 ,
,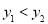 .其中正确的有_______(填序号).
.其中正确的有_______(填序号).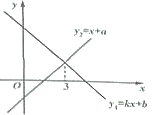
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标.
 ;
;  ;
;  ;
;(3)求出△ABC的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解七年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°,根据图表中提供的信息,回答下列问题:
体育成绩统计表
体育成绩(分)
人数(人)
百分比(%)
26
8
16
27
12
24
28
15
29
n
30
(1)求样本容量及n的值;
(2)已知该校七年级共有500名学生,如果体育成绩达28分以上为优秀,请估计该校七年级学生体育成绩达到优秀的总人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=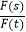 ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知A(0,-2),B(-2,1),C(3,2)
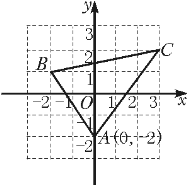
(1)求线段AB、BC、AC的长;
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求A′B′、B′C′、A′C′的长;
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
相关试题

