【题目】如图,在一正方形ABCD中.E为对角线AC上一点,连接EB、ED,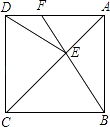
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数.
参考答案:
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴CD=CB,∠DCA=∠BCA,
在△BEC和△DEC中
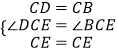
∴△BEC≌△DEC(SAS)
(2)
解:∵∠DEB=140°,
∵△BEC≌△DEC,
∴∠DEC=∠BEC=70°,
∴∠AEF=∠BEC=70°,
∵∠DAB=90°,
∴∠DAC=∠BAC=45°,
∴∠AFE=180°﹣70°﹣45°=65°.
答:∠AFE的度数是65°.
【解析】(1)根据正方形的性质得出CD=CB,∠DCA=∠BCA,根据SAS即可证出结论;(2)根据对顶角相等求出∠AEF,根据正方形的性质求出∠DAC,根据三角形的内角和定理求出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线交于点O,AC=16cm,BD=12cm.

(1)求菱形的边长和面积;
(2)求菱形的高DM. -
科目: 来源: 题型:
查看答案和解析>>【题目】实数0是( )
A.有理数
B.无理数
C.正数
D.负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x+2)(x﹣3)=x+2的解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
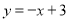 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线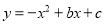 经过B,C两点,点A是抛物线与x轴的另一个交点.
经过B,C两点,点A是抛物线与x轴的另一个交点.
(1)求出点B和点C的坐标.
(2)求此抛物线的函数解析式.
(3)在抛物线x轴上方存在一点P(不与点C重合),使
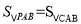 ,请求出点P的坐标.
,请求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据中若最小数与平均数相等,那么这组数据的方差为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
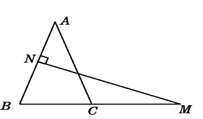
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
相关试题

