【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
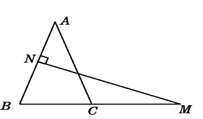
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
参考答案:
【答案】(1) 20°;(2) 35°;
(3)规律:∠NMB=![]() ∠A.
∠A.
【解析】(1)根据等边对等角,由AB=AC可得到∠ABM=∠ACB,再结合已知∠A的度数,即可求出∠NMB的度数;
(2)仿照第(1)问的求解过程即可得到∠NMB的度数;
(3)结合上述两问的解答,即可发现∠NMB和∠A之间的大小关系,然后仿照上述解答过程进行验证即可.
解:(1)∵AB=AC,
∴∠ABM=∠ACB.
∵∠BAC=40°,∠ABM=∠ACB,
∴∠ABM=![]() ×(180°-∠BAC)=70°.
×(180°-∠BAC)=70°.
∵MN是AB的垂直平分线,∠ABM=70°,
∴∠NMB=90°-∠ABM=90°-70°=20°.
(2)与(1)同理可得∠B=![]() ×(180°-∠BAC)=55°,
×(180°-∠BAC)=55°,
∴∠NMB=90°-55°=35°.
(3)规律:在等腰△ABC中,当AB=AC,∠NMB的度数恰好为顶角∠A度数的一半,即∠NMB=![]() ∠A.理由如下:
∠A.理由如下:
∵AB=AC,
∴∠ABM=∠ACB.
∴∠ABM=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∵∠ABM=90°-![]() ∠A,∠BNM=90°,
∠A,∠BNM=90°,
∴∠BMN=90°-∠ABM=![]() ∠A.
∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一正方形ABCD中.E为对角线AC上一点,连接EB、ED,
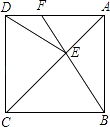
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
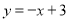 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线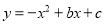 经过B,C两点,点A是抛物线与x轴的另一个交点.
经过B,C两点,点A是抛物线与x轴的另一个交点.
(1)求出点B和点C的坐标.
(2)求此抛物线的函数解析式.
(3)在抛物线x轴上方存在一点P(不与点C重合),使
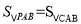 ,请求出点P的坐标.
,请求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据中若最小数与平均数相等,那么这组数据的方差为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于
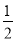 GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.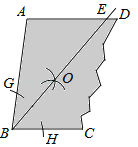
(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a-1)x|a|+2=0是关于x的一元一次方程,则a=____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产某种商品每件成本为20元,这种商品在未来40天内的日销售量y(件)与时间x(天)的关系如下表:
时间x(天)
1
3
6
10
...
日销售量y(件)
94
90
84
76
...
未来40天内,前20天每天的价格m(元/件)与时间x(天)的函数关系式为
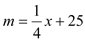 (1≤x≤20),后20天每天的价格为30元/件(21≤x≤40).
(1≤x≤20),后20天每天的价格为30元/件(21≤x≤40).(1)分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的y(件)与x(天)之间的函数关系式.
(2)当1≤x≤20时,设日销售利润为W元,求出W与x的函数关系式.
(3)在未来40天中,哪一天的日销售利润最大,最大日销售利润是多少?
相关试题

