【题目】如图,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 经过B,C两点,点A是抛物线与x轴的另一个交点.
经过B,C两点,点A是抛物线与x轴的另一个交点.

(1)求出点B和点C的坐标.
(2)求此抛物线的函数解析式.
(3)在抛物线x轴上方存在一点P(不与点C重合),使![]() ,请求出点P的坐标.
,请求出点P的坐标.
参考答案:
【答案】(1)B(3,0), C(0,3) (2)![]() (3)P(2,3)
(3)P(2,3)
【解析】(1)已知了过B、C两点的直线的解析式,当x=0时可求出C点的坐标,当y=0是可求出B点的坐标.
(2)由于抛物线的解析式中只有两个待定系数,因此将B、C两点的坐标代入抛物线中即可求出抛物线的解析式.
(3)根据(2)的抛物线的解析式可得出A点的坐标,由此可求出AB的长,由于S△PAB=S△CAB,而AB边为定值.由此可求出P点的纵坐标,然后将P点的纵坐标代入抛物线的解析式中即可求出P点的坐标.
解:(1)因为B,C分别在x轴和y轴上,令x=0,则y=3,令y=0,则x=3,
故C(0,3)、B(3,0)
(2)把B、C两点坐标代入抛物线y=-x2+bx+c得c=3,-9+3b+3=0,
解出:c=3,b=2,
故抛物线的解析式为:y=-x2+2x+3;
(3) 因为点A在抛物线上,又在x轴负半轴,所以求得点A坐标(-1,0)
所以AB=4
得出![]()
此时P点的纵坐标须为3或-3
P点在抛物线上,则:3=-x2+2x+3或-3=-x2+2x+3,
由3=-x2+2x+3解得x=0(此时不存在三角形,舍去)或x=2,此时,P坐标为P1(2,3)
由-3=-x2+2x+3解得x=![]() 或x=
或x=![]() ,此时P坐标为P2(
,此时P坐标为P2(![]() ,-3) ,P3(
,-3) ,P3(![]() ,-3)
,-3)
综上所述,存在点P,使![]() ,坐标分别为P1(2,3), P2(
,坐标分别为P1(2,3), P2(![]() ,-3) ,P3(
,-3) ,P3(![]() ,-3)
,-3)
“点睛”难度系数较大,中考常见题目,考查一次函数及二次函数图象上点的坐标特征,二次函数解析式的确定以及图形面积的求法,注意点P存在不同情况,须要考生分类讨论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数0是( )
A.有理数
B.无理数
C.正数
D.负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x+2)(x﹣3)=x+2的解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一正方形ABCD中.E为对角线AC上一点,连接EB、ED,
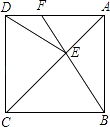
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据中若最小数与平均数相等,那么这组数据的方差为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
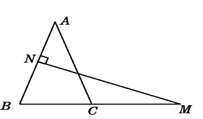
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于
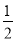 GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.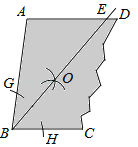
(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
相关试题

