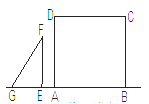
【题目】如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示的位置出发,沿直线AB向右匀速运动,当点G与点B重合时停止运动,设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是( )
A.  B.
B.  C.
C. 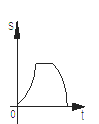 D.
D. 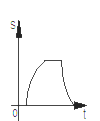
参考答案:
【答案】D
【解析】试题分析:设GE=a,EF=b,AE=m,AB=c,Rt△EFG向右匀速运动的速度为1,
当E点在点A左侧时,S=0。
当点G在点A左侧,点E在点A右侧时,如答图1,

AE=t﹣m,GA=a﹣(t﹣m)=a+m﹣t,
∵PA∥EF,∴△GAP∽△GEF。
∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
∴![]() 。
。
∴S是t的二次函数,且二次项系数为负数,所以抛物线开口向下。
当点G在点A右侧,点E在点B左侧时,S=![]() ab。
ab。
当点G在点B左侧,点E在点B右侧时,如答图2,

GB=a+m+c﹣t,
∵PA∥EF,∴△GBP∽△GEF。
∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
∴![]() 。
。
∴S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上。
综上所述,S与t的图象分为四段,第一段为x轴上的一条线段,第二段为开口向下的抛物线的一部分,第三段为与x轴平行的线段,第四段为开口先上的抛物线的一部分。
故选D。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=6,BC=8.
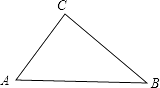
(1)用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.
(2)计算(1)中线段CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C1:y=ax2+bx+
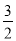 (a≠0)经过点A(-1,0)和B(3,0).
(a≠0)经过点A(-1,0)和B(3,0).
(1)求抛物线C1的解析式,并写出其顶点C的坐标;
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2,此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的下方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标;
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:
①tan∠ENM的值如何变化?请说明理由;
②点M到达点C时,直接写出点P经过的路线长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了深化课程改革,省实验积极开展校本课程建设,计划成立“增量阅读”、“趣味数学”、“音乐舞蹈”和“戏剧英语”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了初中部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向
增量阅读
趣味数学
音乐舞蹈
戏曲英语
其他
所占百分比
a
20%
b
10%
5%
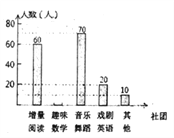
根据统计图表的信息,解答下列问题:
(l)求本次抽样调查的学生总人数及a、b的值:
(2)将条形统计图补充完整;
(3)若该校共有5000名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从
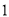 开始,连续的奇数相加,它们和的情况如表所示:
开始,连续的奇数相加,它们和的情况如表所示:加数的个数
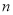
连续奇数的和
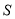
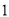
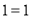
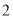
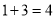
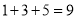
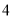
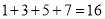
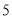
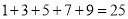
(
 )当
)当时, 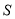 的值为__________.
的值为__________.(
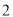 )用含
)用含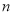 的代数式表示
的代数式表示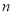 个连续奇数之和
个连续奇数之和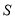 的公式,
的公式, 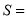 __________.
__________.用含
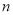 的代数式表示从
的代数式表示从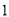 开始的第
开始的第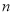 个连续奇数是__________.
个连续奇数是__________.(
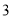 )根据规律计算
)根据规律计算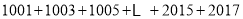 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在①ab是一次单项式;②单项式﹣x2y的系数是﹣1;③3+x2﹣4x是按x的降幂排列的;④数4是单项式;这四句话中不正确的是( )
A.①③
B.②③
C.②④
D.①② -
科目: 来源: 题型:
查看答案和解析>>【题目】某地为了鼓励城区居民节约用水,实行阶梯计价.规定用水收费标准如下:①每户每月的用水量不超过
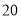 吨时,水费为
吨时,水费为 元/吨时,不超过部分
元/吨时,不超过部分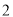 元/吨,超过部分为
元/吨,超过部分为 元/吨.②收取污水处理费
元/吨.②收取污水处理费 元/吨.
元/吨.(
 )若
)若 用户四月份用水
用户四月份用水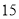 吨,应缴水费__________元.
吨,应缴水费__________元.(
 )若
)若 用户五月份用水
用户五月份用水 吨,缴水费
吨,缴水费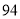 ,求
,求 的值.
的值.(
 )在(
)在(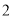 )的条件下,若
)的条件下,若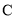 用户某月共缴水费
用户某月共缴水费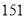 元,求该用户该月用水量.
元,求该用户该月用水量.
相关试题

