【题目】已知抛物线C1:y=ax2+bx+![]() (a≠0)经过点A(-1,0)和B(3,0).
(a≠0)经过点A(-1,0)和B(3,0).

(1)求抛物线C1的解析式,并写出其顶点C的坐标;
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2,此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的下方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标;
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:
①tan∠ENM的值如何变化?请说明理由;
②点M到达点C时,直接写出点P经过的路线长.
参考答案:
【答案】(1)![]() ,顶点C(1,2);(2)F(﹣3,﹣6);(3)①tan∠ENM=2,是定值,不发生变化;②
,顶点C(1,2);(2)F(﹣3,﹣6);(3)①tan∠ENM=2,是定值,不发生变化;②![]() .
.
【解析】试题分析:(1)根据待定系数法即可求得解析式,把解析式化成顶点式即可求得顶点坐标;
(2)根据A、C的坐标求得直线AC的解析式为y=x+1,根据题意求得EF=4,求得EF∥y轴,设F(m,-![]() m2+m+
m2+m+![]() ),则E(m,m+1),从而得出(m+1)-(-
),则E(m,m+1),从而得出(m+1)-(-![]() m2+m+
m2+m+![]() )=4,解方程即可求得F的坐标;
)=4,解方程即可求得F的坐标;
(3)①先求得四边形DFBC是矩形,作EG⊥AC,交BF于G,然后根据△EGN∽△EMC,对应边成比例即可求得tan∠ENM=![]() =2;
=2;
②根据勾股定理和三角形相似求得EN=![]() ,然后根据三角形中位线定理即可求得.
,然后根据三角形中位线定理即可求得.
试题解析:(1)∵抛物线C1:y=ax2+bx+![]() (a≠0)经过点A(-1,0)和B(3,0),
(a≠0)经过点A(-1,0)和B(3,0),
∴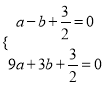 解得
解得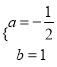 ,
,
∴抛物线C1的解析式为y=-![]() x2+x+
x2+x+![]() ,
,
∵y=-![]() x2+x+
x2+x+![]() =-
=-![]() (x-1)2+2,
(x-1)2+2,
∴顶点C的坐标为(1,2);
(2)如图1,作CH⊥x轴于H,
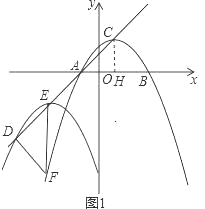
∵A(-1,0),C(1,2),
∴AH=CH=2,
∴∠CAB=∠ACH=45°,
∴直线AC的解析式为y=x+1,
∵△DEF是以EF为底的等腰直角三角形,
∴∠DEF=45°,
∴∠DEF=∠ACH,
∴EF∥y轴,
∵DE=AC=2![]() ,
,
∴EF=4,
设F(m,-![]() m2+m+
m2+m+![]() ),则E(m,m+1),
),则E(m,m+1),
∴(m+1)-(-![]() m2+m+
m2+m+![]() )=4,
)=4,
解得m=3(舍)或m=-3,
∴F(-3,-6);
(3)①tan∠ENM的值为定值,不发生变化;
如图2,
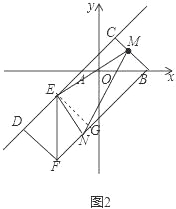
∵DF⊥AC,BC⊥AC,
∴DF∥BC,
∵DF=BC=AC,
∴四边形DFBC是矩形,
作EG⊥AC,交BF于G,
∴EG=BC=AC=2![]() ,
,
∵EN⊥EM,
∴∠MEN=90°,
∵∠CEG=90°,
∴∠CEM=∠NEG,
∴△ENG∽△EMC,
∴![]() ,
,
∵F(-3,-6),EF=4,
∴E(-3,-2),
∵C(1,2),
∴EC=![]() =4
=4![]() ,
,
∴![]() =2,
=2,
∴tan∠ENM=![]() =2;
=2;
∵tan∠ENM的值为定值,不发生变化;
②点P经过的路径是线段P1P2,如图3,
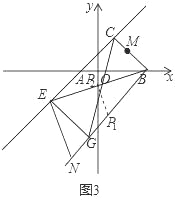
∵四边形BCEG是矩形,GP2=CP2,
∴EP2=BP2,
∵△EGN∽△ECB,
∴![]() ,
,
∵EC=4![]() ,EG=BC=2
,EG=BC=2![]() ,
,
∴EB=2![]() ,
,
∴![]() ,
,
∴EN=![]() ,
,
∵P1P2是△BEN的中位线,
∴P1P2=![]() EN=
EN=![]() ;
;
∴点M到达点C时,点P经过的路线长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, 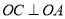 ,
, 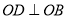 .
.(
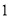 )根据所给的条件用量角器和三角板画出图形.
)根据所给的条件用量角器和三角板画出图形.(
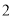 )求
)求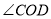 的度数.
的度数.(注意:可能存在不同的情形)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某居民小区为了解小区500户居民家庭平均月使用塑料袋的数量情况,随机调查了10户居民家庭月使用塑料袋的数量,结果如下(单位:只):65,70,85,74,86,78,74,92,82,94.
根据统计情况,估计该小区这500户家庭每月一共使用塑料袋_________只.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=6,BC=8.
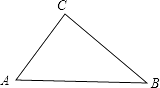
(1)用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.
(2)计算(1)中线段CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了深化课程改革,省实验积极开展校本课程建设,计划成立“增量阅读”、“趣味数学”、“音乐舞蹈”和“戏剧英语”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了初中部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向
增量阅读
趣味数学
音乐舞蹈
戏曲英语
其他
所占百分比
a
20%
b
10%
5%
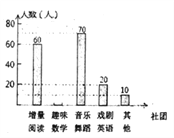
根据统计图表的信息,解答下列问题:
(l)求本次抽样调查的学生总人数及a、b的值:
(2)将条形统计图补充完整;
(3)若该校共有5000名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示的位置出发,沿直线AB向右匀速运动,当点G与点B重合时停止运动,设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是( )
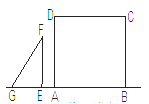
A.
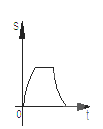 B.
B. 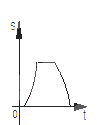 C.
C. 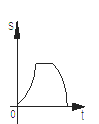 D.
D. 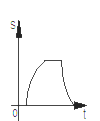
-
科目: 来源: 题型:
查看答案和解析>>【题目】从
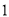 开始,连续的奇数相加,它们和的情况如表所示:
开始,连续的奇数相加,它们和的情况如表所示:加数的个数
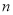
连续奇数的和
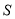
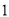
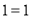
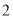
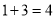
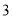
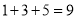
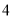
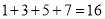
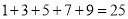
(
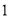 )当
)当时, 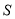 的值为__________.
的值为__________.(
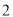 )用含
)用含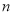 的代数式表示
的代数式表示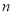 个连续奇数之和
个连续奇数之和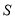 的公式,
的公式, 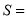 __________.
__________.用含
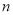 的代数式表示从
的代数式表示从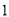 开始的第
开始的第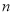 个连续奇数是__________.
个连续奇数是__________.(
 )根据规律计算
)根据规律计算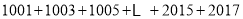 .
.
相关试题

