【题目】如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0),与y轴相交于点C(0,3).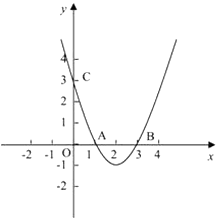
(1)求抛物线的函数关系式.
(2)将y=ax2+bx+c化成y=a(x﹣m)2+k的形式(请直接写出答案).
(3)若点D(3.5,m)是抛物线y=ax2+bx+c上的一点,请求出m的值,并求出此时△ABD的面积.
参考答案:
【答案】
(1)解:由已知得 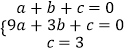 ,解得
,解得 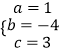 ,
,
∴y=x2﹣4x+3;
(2)解:y= x2﹣4x+3 =( x2﹣4x+4)-1= (x-1)2﹣1;
(3)解:∵ ![]() 是抛物线y=x2﹣4x+3上的点,
是抛物线y=x2﹣4x+3上的点,
∴ ![]() ;
;
∴ ![]() .
.
【解析】(1)利用待定系数法将A、B、C三点坐标代入所设函数解析式,建立方程组求解即可;或根据A、B两点是抛物线与x轴的交点坐标,因此设函数解析式为y=a(x-1)(x-3),再将点C的坐标代入求解,即可求出将函数解析式。
(2)通过配方法将函数解析式化成顶点式即可。
(3)将x=3.5代入函数解析式求出点D的纵坐标,即可得出点D的坐标,再根据点A、B、D的坐标求出△ABD的面积即可。
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.),还要掌握三角形的面积(三角形的面积=1/2×底×高)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
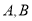 的坐标分别是点
的坐标分别是点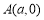 ,
, ,且
,且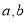 满足:
满足: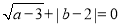 .
.(1)则
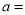 _________,
_________,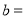 _________;
_________;(2)
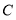 为
为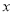 轴负半轴上一点,过点
轴负半轴上一点,过点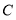 作
作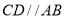 交
交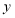 轴于点
轴于点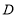 .
.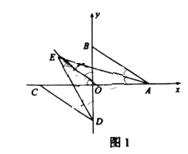
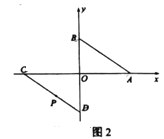
①如图1,
 与
与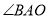 的角平分线交于点
的角平分线交于点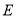 ,求
,求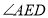 的度数;
的度数;②如图2,点
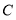 的坐标为
的坐标为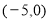 ,点
,点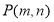 为线段
为线段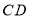 上一点,求
上一点,求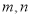 之间满足的关系式.
之间满足的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
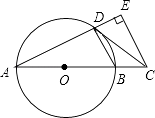
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解. 根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.x
…
﹣3
﹣

﹣2
﹣

﹣1
﹣

0

1

2
…
y
…
﹣8
﹣
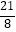
0

m
﹣

﹣2
﹣
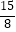
0
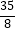
12
…
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有个,分别为;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集. -
科目: 来源: 题型:
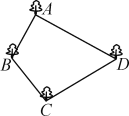
查看答案和解析>>【题目】张大伯承包了一个四边形的池塘,如图所示,它的四个角A,B,C,D处均有一棵大树,张大伯今年养鱼喜获丰收,明年准备把池塘面积扩大一倍,但又不想毁掉这四棵大树,并且扩建后的池塘呈平行四边形形状.张大伯这一设想是否能实现?请你帮助他解决一下,并画出草图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣4x+3.

(1)求函数图象的对称轴、顶点坐标、与坐标轴交点的坐标,并画出函数的大致图象;
(2)根据图象直接写出函数值y为负数时,自变量x的取值范围.
相关试题

