【题目】在平面直角坐标系中,点![]() 的坐标分别是点
的坐标分别是点![]() ,
,![]() ,且
,且![]() 满足:
满足:![]() .
.
(1)则![]() _________,
_________,![]() _________;
_________;
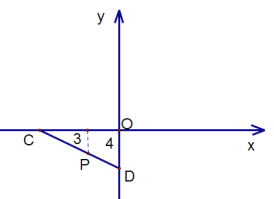
(2)![]() 为
为![]() 轴负半轴上一点,过点
轴负半轴上一点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .
.
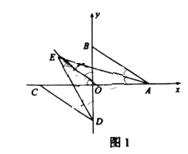
①如图1,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,求
,求![]() 的度数;
的度数;
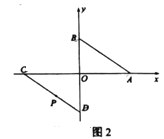
②如图2,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 上一点,求
上一点,求![]() 之间满足的关系式.
之间满足的关系式.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)利用绝对值和二次根式的非负性可得a、b的值;
(2)①如下图,根据![]() 和
和![]() ,可得∠CDO+∠BAO=90°,从而推导得出∠AED;
,可得∠CDO+∠BAO=90°,从而推导得出∠AED;
②如下图,将直线![]() 平移到
平移到![]() 处,
处,![]() 对应
对应![]() ,
,![]() 对应
对应![]() ,根据△COD的面积关系,可得出点D的坐标;然后在△COD的面积还等于③+④可得到m、n的关系.
,根据△COD的面积关系,可得出点D的坐标;然后在△COD的面积还等于③+④可得到m、n的关系.
(1)∵![]()
∴![]()
∴![]() ,
,![]()
(2)①分别作![]() ,
,![]() .
.
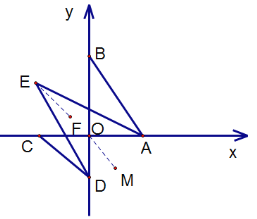
则![]() ,
,![]() .
.
设∠CDE=x,∠BAE=y
∴![]()
∴![]()
则![]() .
.
②设![]() .
.
将直线![]() 平移到
平移到![]() 处,
处,![]() 对应
对应![]() ,
,![]() 对应
对应![]()
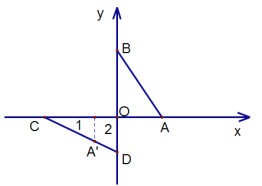
则![]()
已知![]() 、
、![]() 坐标,则直线
坐标,则直线![]() 与
与![]() 轴交点为
轴交点为![]() .
.
由![]() 可得:
可得:![]() .
.
根据![]() ,即:
,即:![]()
解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG.
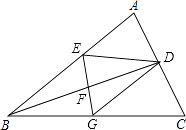
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2,求GC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( )
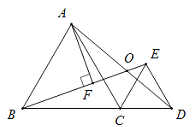
A. 1 B.
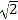 C.
C. 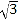 D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:

(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格? -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.
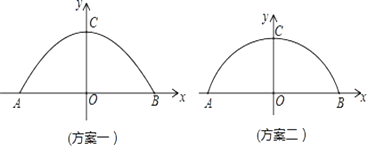
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
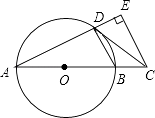
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0),与y轴相交于点C(0,3).
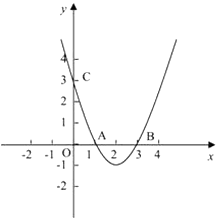
(1)求抛物线的函数关系式.
(2)将y=ax2+bx+c化成y=a(x﹣m)2+k的形式(请直接写出答案).
(3)若点D(3.5,m)是抛物线y=ax2+bx+c上的一点,请求出m的值,并求出此时△ABD的面积.
相关试题

