【题目】如图,抛物线y=x2﹣3x+ ![]() 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E 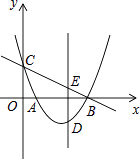
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
参考答案:
【答案】
(1)解:∵抛物线y=x2﹣3x+ ![]() 与x轴相交于A、B两点,与y轴相交于点C,
与x轴相交于A、B两点,与y轴相交于点C,
∴令y=0,可得x= ![]() 或x=
或x= ![]() ,
,
∴A( ![]() ,0),B(
,0),B( ![]() ,0);
,0);
令x=0,则y= ![]() ,
,
∴C点坐标为(0, ![]() ),
),
设直线BC的解析式为:y=kx+b,则有,
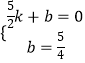 ,
,
解得: 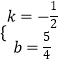 ,
,
∴直线BC的解析式为:y=- ![]() x+
x+ ![]() ;
;
(2)解:设点D的横坐标为m,则坐标为(m, ![]() ),
),
∴E点的坐标为(m, ![]() m+
m+ ![]() ),
),
设DE的长度为d,
∵点D是直线BC下方抛物线上一点,
则d= ![]() m+
m+ ![]() ﹣(m2﹣3m+
﹣(m2﹣3m+ ![]() ),
),
整理得,d=﹣m2+ ![]() m,
m,
∵a=1>0,
∴当m=﹣ ![]() =
= ![]() 时,d最大=
时,d最大= ![]() =
= ![]() =
= ![]() ,
,
∴D点的坐标为( ![]() ,
, ![]() ).
).
【解析】(1)利用坐标轴上点的特点求出A、B、C点的坐标,再用待定系数法求得直线BC的解析式;(2)设点D的横坐标为m,则纵坐标为(m, ![]() ),E点的坐标为(m,
),E点的坐标为(m, ![]() ),可得两点间的距离为d=
),可得两点间的距离为d= ![]() ,利用二次函数的最值可得m,可得点D的坐标.
,利用二次函数的最值可得m,可得点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,并且AE=
 (AB+AD),求∠ABC+∠ADC的度数.
(AB+AD),求∠ABC+∠ADC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个边长为4的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E.

(1)求CE的长;
(2)求阴影部分的面积. -
科目: 来源: 题型:
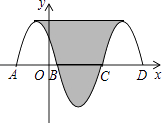
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1 , 将Cl绕点B中心对称变换得C2 , C2与x轴交于另一点C,将C2绕点C中心对称变换得C3 , 连接C,与C3的顶点,则图中阴影部分的面积为( )
A.32
B.24
C.36
D.48 -
科目: 来源: 题型:
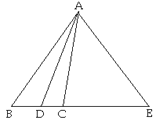
查看答案和解析>>【题目】如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗?为什么?
(2)若∠B=50°,∠CAD︰∠E=1︰3,求∠E的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=
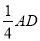 ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.

相关试题

