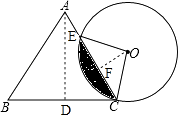
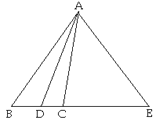
【题目】一个边长为4的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E. 
(1)求CE的长;
(2)求阴影部分的面积.
参考答案:
【答案】
(1)解:如图,过点A作AD⊥BC于点D,
∵三角形ABC为等边三角形,且AB=BC=4,
∴BD= ![]() BC=2,∠ACB=60°,
BC=2,∠ACB=60°,
∴AD= ![]() =
= ![]() =2
=2 ![]() ,
,
∵等边三角形ABC与⊙O等高,且⊙O与BC相切于点C,
∴OC= ![]() AD=
AD= ![]() ,∠OCD=90°,
,∠OCD=90°,
过点O作OF⊥CE于点F,
∴∠OCF=∠OCD﹣∠ACB=30°,
∴CF=OCcos∠OCF= ![]() ×
× ![]() =
= ![]() ,
,
则CE=2CF=3;
(2)解:由(1)知OF⊥CE,∠OCF=30°,
∴∠COF=60°,OF=OCsin∠OCF= ![]() ,
,
∴∠COE=120°,
则S阴影=S扇形COE﹣S△COE
= ![]() ﹣
﹣ ![]() ×3×
×3× ![]()
=π﹣ ![]() .
.
【解析】(1)作AD⊥BC,由等腰三角形的性质可得BD=2,根据勾股定理得出AD=2 ![]() ,结合等边三角形ABC与⊙O等高且⊙O与BC相切于点C得OC=
,结合等边三角形ABC与⊙O等高且⊙O与BC相切于点C得OC= ![]() 、∠OCD=90°,作OF⊥CE于点F,从而知∠OCF=30°,利用三角函数求得CF的长,最后根据勾股定理得CE=2CF;(2)由(1)知OF⊥CE、∠OCF=30°从而得∠COF=60°、OF=OCsin∠OCF=
、∠OCD=90°,作OF⊥CE于点F,从而知∠OCF=30°,利用三角函数求得CF的长,最后根据勾股定理得CE=2CF;(2)由(1)知OF⊥CE、∠OCF=30°从而得∠COF=60°、OF=OCsin∠OCF= ![]() ,继而知∠COE=120°,根据S阴影=S扇形COE﹣S△COE可得答案.
,继而知∠COE=120°,根据S阴影=S扇形COE﹣S△COE可得答案.
【考点精析】本题主要考查了等边三角形的性质和切线的性质定理的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
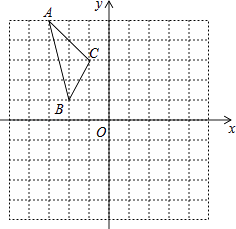
(1)若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 , 写出△A3B3C3的各顶点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,并且AE=
 (AB+AD),求∠ABC+∠ADC的度数.
(AB+AD),求∠ABC+∠ADC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣3x+
 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E 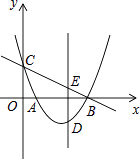
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标. -
科目: 来源: 题型:
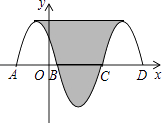
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1 , 将Cl绕点B中心对称变换得C2 , C2与x轴交于另一点C,将C2绕点C中心对称变换得C3 , 连接C,与C3的顶点,则图中阴影部分的面积为( )
A.32
B.24
C.36
D.48 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗?为什么?
(2)若∠B=50°,∠CAD︰∠E=1︰3,求∠E的度数.
相关试题

