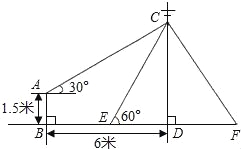
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).
参考答案:
【答案】拉线CE的长约为5.7米
【解析】
试题分析:由题意可先过点A作AH⊥CD于H.在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
试题解析:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH=![]() ,
,
∴CH=AHtan∠CAH,
∴CH=AHtan∠CAH=6tan30°=6×![]() (米),∵DH=1.5,∴CD=2
(米),∵DH=1.5,∴CD=2![]() +1.5,
+1.5,
在Rt△CDE中,∵∠CED=60°,sin∠CED=![]() ,
,
∴CE=![]() =4+
=4+![]() ≈5.7(米),
≈5.7(米),
答:拉线CE的长约为5.7米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2y﹣y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据:1,2,4,3,2,4,2,5,6,1,它们的平均数为_______,众数为_______,中位数为_______.
-
科目: 来源: 题型:
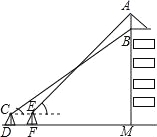
查看答案和解析>>【题目】为了弘扬南开精神,我校将“允公允能,日新月异”的校调印在旗帜上,放置在教学楼的顶部(如图所示),小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)补全△A′B′C′根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积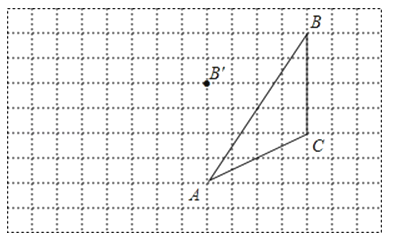
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船在A,B两个码头之间航行,顺水航行需3h,逆水航行需5h.已知水流速度为4km/h,求轮船在静水中的航行速度.若设轮船在静水中的航行速度为xkm/h,则可列式为( )
A. 3x+4=5x﹣4 B. 3(4+x)=5(4﹣x)
C. 3(x+4)=5(x﹣4) D. 3(x﹣4)=5(x+4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE.其中正确的是( )

A. ② B. ①②③ C. ①②④ D. ①②③④
相关试题

