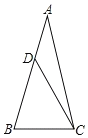
【题目】如图,△ABC中,AB=AC,∠A=30°,点D在边AB上,∠ACD=15°,则![]() ____.
____.
参考答案:
【答案】![]() .
.
【解析】
根据题意作CE⊥AB于E,作DF⊥AC于F,在CF上截取一点H,使得CH=DH,连接DH,并设AD=2x,解直角三角形求出BC(用x表示)即可解决问题.
解:作CE⊥AB于E,作DF⊥AC于F,在CF上截取一点H,使得CH=DH,连接DH.
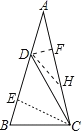
设AD=2x,
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,DF![]() AD=x,AF
AD=x,AF![]() x,
x,
∵∠ACD=15°,HD=HC,
∴∠HDC=∠HCD=15°,
∴∠FHD=∠HDC+∠HCD=30°,
∴DH=HC=2x,FH![]() x,
x,
∴AB=AC=2x+2![]() x,
x,
在Rt△ACE中,EC![]() AC=x
AC=x![]() x,AE
x,AE![]() EC
EC![]() x+3x,
x+3x,
∴BE=AB﹣AE![]() x﹣x,
x﹣x,
在Rt△BCE中,BC![]() 2
2![]() x,
x,
∴![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
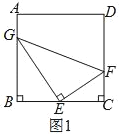
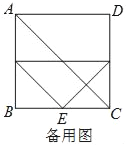
查看答案和解析>>【题目】如图1,正方形ABCD的边长为4,把三角板的直角顶点放置BC中点E处,三角板绕点E旋转,三角板的两边分别交边AB、CD于点G、F.
(1)求证:△GBE∽△GEF.
(2)设AG=x,GF=y,求Y关于X的函数表达式,并写出自变量取值范围.
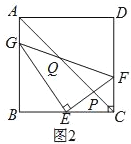
(3)如图2,连接AC交GF于点Q,交EF于点P.当△AGQ与△CEP相似,求线段AG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠C=90°,AC=8,BC=6,角平分线AD、BE相交于点O,则四边形OECD的面积为( )
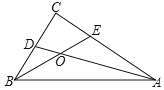
A.5B.
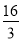 C.
C.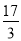 D.8
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是边长为2的等边三角形,点P为直线BC上的动点,把线段AP绕A点逆时针旋转60°至AE,O为AB边上一动点,则OE的最小值为____.
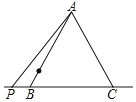
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AH∥CG,且分别交对角线BD于H、G,连接CH和AG,求证:∠CHG=∠AGH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
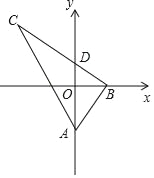
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC为等边三角形,O为BC的中点,D、E分别在边AB、AC上.如图1.
(1)若∠DOE=120°,求证:OD=OE;
(2)如图2,BD=4,CE=2,M是DE的中点,求OM的长.
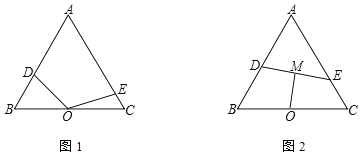
相关试题

