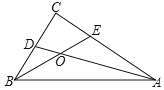
【题目】△ABC中,∠C=90°,AC=8,BC=6,角平分线AD、BE相交于点O,则四边形OECD的面积为( )
A.5B.![]() C.
C.![]() D.8
D.8
参考答案:
【答案】C
【解析】
由题意作OM⊥AB于M,OJ⊥BC于J,OK⊥AC于K,DH⊥BC于H,连接OC,并根据题意分别求出CD,CE,OJ,OK即可解决问题.
解:如图,作OM⊥AB于M,OJ⊥BC于J,OK⊥AC于K,DH⊥BC于H,连接OC.
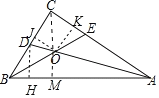
在Rt△ABC中,
∵∠ACB=90°,AC=8,BC=6,
∴AB=10,
∵点O是△ABC的内心,
∴OM=OJ=OK![]() 2,
2,
∵∠DCA=∠DHA=90°,AD=AD(公共边),∠DAC=∠DAH,
∴△DAC≌△DAH(AAS),
∴CD=DH,AC=AH=8,
∴BH=10﹣8=2,
设CD=DH=x,
在Rt△BDH中,
∵BD2=BH2+DH2,
∴(6﹣x)2=x2+22,
∴x![]() ,
,
同法可求:EC=3,
∴S四边形CDOE=S△COD+S△COE![]() CDOJ
CDOJ![]() ECOK
ECOK![]() 2
2![]() 3×2
3×2![]() .
.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q、R处,且相距30海里.如果知道“远航”号沿东北方向航行,则“海天”号沿( )方向航行.

A.西南B.东北C.西北D.东南
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,
 ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
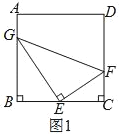
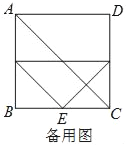
查看答案和解析>>【题目】如图1,正方形ABCD的边长为4,把三角板的直角顶点放置BC中点E处,三角板绕点E旋转,三角板的两边分别交边AB、CD于点G、F.
(1)求证:△GBE∽△GEF.
(2)设AG=x,GF=y,求Y关于X的函数表达式,并写出自变量取值范围.
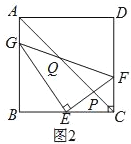
(3)如图2,连接AC交GF于点Q,交EF于点P.当△AGQ与△CEP相似,求线段AG的长.
-
科目: 来源: 题型:
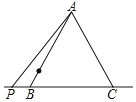
查看答案和解析>>【题目】△ABC是边长为2的等边三角形,点P为直线BC上的动点,把线段AP绕A点逆时针旋转60°至AE,O为AB边上一动点,则OE的最小值为____.
-
科目: 来源: 题型:
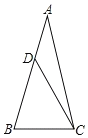
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=30°,点D在边AB上,∠ACD=15°,则
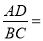 ____.
____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AH∥CG,且分别交对角线BD于H、G,连接CH和AG,求证:∠CHG=∠AGH.

相关试题

