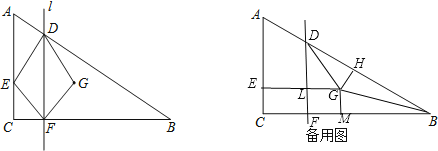
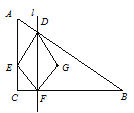
【题目】如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,点E、F同时从点C出发,以![]() cm/s的速度分别沿CA、CB匀速运动,当点E到达点 A时,两点同时停止运动,设运动时间为ts.过点F作BC的垂线l交AB于点D,点G与点E关于直线l对称.
cm/s的速度分别沿CA、CB匀速运动,当点E到达点 A时,两点同时停止运动,设运动时间为ts.过点F作BC的垂线l交AB于点D,点G与点E关于直线l对称.
(1)当t = s时,点G在∠ABC的平分线上;
(2)当t = s时,点G在AB边上;
(3)设△DFG与△DFB重合部分的面积为Scm2, 求S与t之间的函数关系式,并写出t的取值范围.

参考答案:
【答案】(1)![]() (2)
(2)![]() (3)①
(3)①![]() =
= ![]() ②
②![]()
【解析】试题分析:(1)过点G做GH⊥BD,垂足为H,GM⊥FB,垂足为M,点E、F同时从点C出发,所以EC=CF=FM=GM=GH=![]() t,且DG也是△BDF的角平分线,由△BDF∽△ABC得:
t,且DG也是△BDF的角平分线,由△BDF∽△ABC得: ![]() ,∴BD=5
,∴BD=5![]() t,DF=3
t,DF=3![]() t,可求得DL、BM的长度,由DL=DH,BH=BM,构造关于t的方程可以求得答案.
t,可求得DL、BM的长度,由DL=DH,BH=BM,构造关于t的方程可以求得答案.
(2)点G在AB边上时,过点G作GH⊥BC,垂足为H,由(1)中的数值,结合△BGH∽△BAC,构造出关于t的方程,可以得到答案.
(3))由DF∥AC得到△ABC∽△DBF,∴ ![]() ,即
,即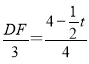 ,得到DF=
,得到DF=![]() (8t),分两种情况讨论:
(8t),分两种情况讨论:
①当0<t≤![]() 时,S=S△DFG=S△DEF=
时,S=S△DFG=S△DEF=![]() DFCF=
DFCF=![]() ×
×![]() (8t)×
(8t)×![]() t=
t=![]() t2+
t2+![]() t;
t;
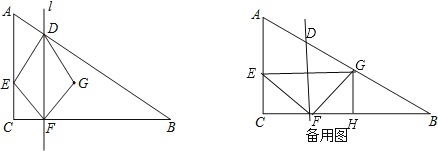
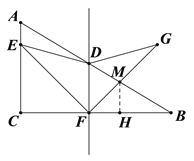
②当![]() <t≤6时,设G交AB于点M,过点M作MH⊥BC于H,设FH=MH=a,求得BH,解出a与t的关系,继而求得S与t的关系.
<t≤6时,设G交AB于点M,过点M作MH⊥BC于H,设FH=MH=a,求得BH,解出a与t的关系,继而求得S与t的关系.
试题解析:(1)![]()
设DF,EG相交于L,过点G做GH⊥BD,垂足为H,GM⊥FB,垂足为M,点E、F同时从点C出发,所以四边形ECFL、四边形LFGM都是正方形,
∴EC=CF=FM=GM=GH=![]() t,
t,
又∵DG也是△BDF的角平分线,
∴DL=DH,
∵DF∥AC,
∴△BDF∽△BAC,
∴![]() ,
,
∴BD=5![]() t,DF=3
t,DF=3![]() t,
t,
又∵DL=DH=3![]() t
t![]() t=3
t=3![]() t,
t,
BH=BM=4-t,又∵BD=BH+HD,
∴5![]() t=3
t=3![]() t+4t,解得:t=
t+4t,解得:t=![]() .
.
(2)![]()
点G在AB边上时,过点G作GH⊥BC,垂足为H,
∵GH∥AC,
所以△BGH∽△BAC,
∴![]() ,即:
,即: 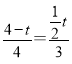 ,
,
解得:t=![]() .
.
(3)∵DF∥AC
∴△ABC∽△DBF,
∴![]() ,
,
即 ,解得
,解得![]()
①当![]() 时,
时,
![]() =
= ![]()
②当![]() 时,设FG交AB于点M,过点M作MH⊥BC于H,设FH=MH=a,
时,设FG交AB于点M,过点M作MH⊥BC于H,设FH=MH=a,
则BH= ![]() ,
,
∴![]() ,
,
解得![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列语句中:①无理数的相反数是无理数;②一个数的绝对值一定是非负数;③有理数比无理数小;④无限小数不一定是无理数.其中正确的是( )
A. ②③ B. ②③④ C. ①②④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读第(1)题的解答过程,然后再解第(2)题.
(1)已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x2+ax+b),
则:2x3﹣x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得 , 解得
, 解得 , ∴
, ∴
解法二:设2x3﹣x2+m=A(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取 ,
,
2× =0,故
=0,故  .
.
(2)已知x4+mx3+nx﹣16有因式(x﹣1)和(x﹣2),求m、n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数
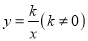 在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1。直线l过O、E两点,则tan∠EOC的值为( )
在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1。直线l过O、E两点,则tan∠EOC的值为( ) 
A.
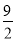 B. 5 C.
B. 5 C.  D. 3
D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在A岛周围25海里水域有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°方向,轮船继续前行20海里到达B处发现A岛在北偏东45°方向,该船若不改变航向继续前进,有无触礁的危险?(参考数据:
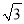 ≈1.732)
≈1.732)
相关试题

