搜索
【题目】如图所示，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数
在第一象限的图象经过顶点A(m，m+3)和CD上的点E，且OB-CE=1。直线l过O、E两点，则tan∠EOC的值为( )
A. 
B. 5 C. 
D. 3
参考答案：
【答案】C
【解析】分析：本题利用正方形的边长相等和点A的坐标求出点E的坐标，再根据OB-CE=1，求出m的值，即可求出OC、CE的长，从而求出tan∠EOC.
解析：∵A(m，m+3)，∴OA=m,AB=m+3，∵正方形ABCD，∴BC=AB= m+3，∴C点的横坐标为2m+3,∵点A，点E都在
上，∴E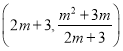
，∵OB-CE=1，∴
(舍去)，∴CE=2,OC=9, ∴ tan∠EOC= 
.
故选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读第（1）题的解答过程，然后再解第（2）题．
（1）已知多项式2x3﹣x2+m有一个因式是2x+1，求m的值．
解法一：设2x3﹣x2+m=（2x+1）（x2+ax+b），
则：2x3﹣x2+m=2x3+（2a+1）x2+（a+2b）x+b
比较系数得
， 解得
， ∴
解法二：设2x3﹣x2+m=A（2x+1）（A为整式）
由于上式为恒等式，为方便计算了取
，
2×
=0，故 ．
（2）已知x4+mx3+nx﹣16有因式（x﹣1）和（x﹣2），求m、n的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠C＝90°，AC＝3cm，BC＝4cm，点E、F同时从点C出发，以
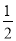cm/s的速度分别沿CA、CB匀速运动，当点E到达点 A时，两点同时停止运动，设运动时间为ts．过点F作BC的垂线l交AB于点D，点G与点E关于直线l对称．（1）当t ＝ s时，点G在∠ABC的平分线上；
（2）当t ＝ s时，点G在AB边上；
（3）设△DFG与△DFB重合部分的面积为Scm2， 求S与t之间的函数关系式，并写出t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”．它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如它的每一行的数字正好对应了（a+b）n（n为非负整数）的展开式中a按次数从大到小排列的项的系数．例如，（a+b）2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字；再如，（a+b）3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字．请认真观察此图，写出（a+b）4的展开式，（a+b）4= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在A岛周围25海里水域有暗礁，一轮船由西向东航行到O处时，发现A岛在北偏东60°方向，轮船继续前行20海里到达B处发现A岛在北偏东45°方向，该船若不改变航向继续前进，有无触礁的危险?（参考数据：
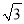≈1.732）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”．它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如它的每一行的数字正好对应了（a+b）n（n为非负整数）的展开式中a按次数从大到小排列的项的系数．例如，（a+b）2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字；再如，（a+b）3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字．请认真观察此图，写出（a+b）4的展开式，（a+b）4= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校开展了“我读书，我快乐”为主题的调查活动，其中七年级二班全体同学一个学期平均一天阅读课外书籍所用时间的情况如下表：
时间（小时）
0.5
1
1.5
2
5
人数（名）
7人
18人
12人
3人
由于填表的同学不小心把墨水滴在了表上，致使表中数据不完整，但知道所用时间为1小时的人数为全班人数的36%．结合上表回答下列问题：
（1）七年级二班共有多少人？
（2）学生所用时间的众数和中位数分别为多少小时？
（3）如果把该班的学生的所用时间情况绘成扇形统计图，则所用时间为2小时的人数所对应的扇形圆心角为多少度？
相关试题
