搜索
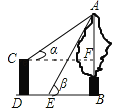
【题目】如图，CD是一高为4米的平台，AB是与CD底部相平的一棵树，在平台顶C点测得树顶A点的仰角α=30°，从平台底部向树的方向水平前进3米到达点E，在点E处测得树顶A点的仰角β=60°，求树高AB（结果保留根号）
参考答案：
【答案】
．
【解析】
试题分析：作CF⊥AB于点F，设AF=x米，在直角△ACF中利用三角函数用x表示出CF的长，在直角△ABE中表示出BE的长，然后根据CF﹣BE=DE即可列方程求得x的值，进而求得AB的长．
试题解析：作CF⊥AB于点F，设AF=x米，在Rt△ACF中，tan∠ACF=
，则CF=
=
，在直角△ABE中，AB=x+BF=4+x（米），在直角△ABF中，tan∠AEB=
，则BE=
=
（x+4）米．
∵CF﹣BE=DE，即
．解得：x=
，则AB=+4=（米）．
答：树高AB是米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列方程：
（1）（x﹣5）2=8（x﹣5）
（2）2x2﹣4x﹣3=0． -
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读第（1）题的解答过程，然后再解第（2）题．
（1）已知多项式2x3﹣x2+m有一个因式是2x+1，求m的值．
解法一：设2x3﹣x2+m=（2x+1）（x2+ax+b），
则：2x3﹣x2+m=2x3+（2a+1）x2+（a+2b）x+b
比较系数得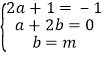
， 解得
， ∴
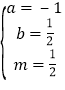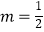
解法二：设2x3﹣x2+m=A（2x+1）（A为整式）
由于上式为恒等式，为方便计算了取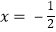
，
2×
=0，故 ．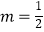
（2）已知x4+mx3+nx﹣16有因式（x﹣1）和（x﹣2），求m、n的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】在下列语句中：①无理数的相反数是无理数；②一个数的绝对值一定是非负数；③有理数比无理数小；④无限小数不一定是无理数．其中正确的是（ ）
A. ②③ B. ②③④ C. ①②④ D. ②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读第（1）题的解答过程，然后再解第（2）题．
（1）已知多项式2x3﹣x2+m有一个因式是2x+1，求m的值．
解法一：设2x3﹣x2+m=（2x+1）（x2+ax+b），
则：2x3﹣x2+m=2x3+（2a+1）x2+（a+2b）x+b
比较系数得
， 解得
， ∴
解法二：设2x3﹣x2+m=A（2x+1）（A为整式）
由于上式为恒等式，为方便计算了取
，
2×
=0，故 ．
（2）已知x4+mx3+nx﹣16有因式（x﹣1）和（x﹣2），求m、n的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠C＝90°，AC＝3cm，BC＝4cm，点E、F同时从点C出发，以
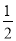cm/s的速度分别沿CA、CB匀速运动，当点E到达点 A时，两点同时停止运动，设运动时间为ts．过点F作BC的垂线l交AB于点D，点G与点E关于直线l对称．（1）当t ＝ s时，点G在∠ABC的平分线上；
（2）当t ＝ s时，点G在AB边上；
（3）设△DFG与△DFB重合部分的面积为Scm2， 求S与t之间的函数关系式，并写出t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”．它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如它的每一行的数字正好对应了（a+b）n（n为非负整数）的展开式中a按次数从大到小排列的项的系数．例如，（a+b）2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字；再如，（a+b）3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字．请认真观察此图，写出（a+b）4的展开式，（a+b）4= ．
相关试题
