【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径。
(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段AC,同时我们还发现损矩形中有公共边的两个三角形角的特点,在公共边的同侧的两个角是相等的。如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC。请再找一对这样的角来 =
(2)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由。
(3)在第(2)题的条件下,若此时AB=![]() ,BD=
,BD=![]() ,求BC的长。
,求BC的长。

参考答案:
【答案】(1)∠ABD=∠ACD;(2)四边形ACEF为正方形,理由见解析;(3)5.
【解析】
(1)以AD为公共边,有∠ABD=∠ACD;
(2)证明△ADC是等腰直角三角形,得AD=CD,则AE=CF,根据对角线相等的菱形是正方形可得结论;
(3)如图2,作辅助线构建直角三角形,证明△ABC≌△CHE,得CH=AB=3,根据平行线等分线段定理可得BG=GH=4,从而得结论.
解:(1)由图1得:△ABD和△ADC有公共边AD,在AD同侧有∠ABD和∠ACD,此时∠ABD=∠ACD;
(2)四边形ACEF为正方形,理由是:
∵∠ABC=90°,BD平分∠ABC,
∴∠ABD=∠CBD=45°
∴∠DAC=∠CBD=45°
∵四边形ACEF是菱形,
∴AELCF,
∴∠ADC=90°,
∴△ADC是等腰直角三角形,
∴AD=CD,.AE=CF,
∴菱形ACEF是正方形;
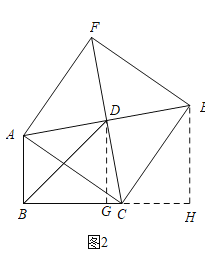
(3)如图2,过D作DG⊥BC于G,过E作EH⊥BC,交BC的延长线于H,
∵∠DBG=45°,
∴△BDG是等腰直角三角形,BD=4![]() ,
,
∵BG=4,四边形ACEF是正方形,
∴AC=CE,∠ACE=90°,AD=DE,
易得△ABC≌△CHE,
∴CH=AB=3,AB//DG//EH,AD=DE,
∴BG=GH=4,
∴CG=4-3=1,
∴BC=BG+CG=4+1=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式
直接销售
粗加工后销售
精加工后销售
每吨获利(元)
100
250
450
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨和粗加工蔬菜16吨(两种加工不能同时进行)。
(1)如果要求在18天内全部销售这140吨蔬菜,请完成下列表格:
销售方式
全部直接销售
全部粗加工后销售
尽量精加工,剩余部分直接销售
获利(元)
(2)如果先进行精加工,来不及精加工的进行粗加工,要求15天内刚好加工完这140吨蔬菜,则应如何分配加工时间?
-
科目: 来源: 题型:
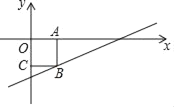
查看答案和解析>>【题目】如图所示,在第四象限内的矩形OABC,两边在坐标轴上,一个顶点在一次函数y=0.5x﹣3的图象上,当点A从左向右移动时,矩形的周长与面积也随之发生变化,设线段OA的长为m,矩形的周长为C,面积为S.
(1)试分别写出C、S与m的函数解析式,它们是否为一次函数?
(2)能否求出当m取何值时,矩形的周长最大?为什么?
-
科目: 来源: 题型:
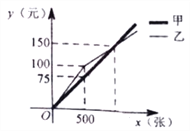
查看答案和解析>>【题目】某社区准备进行“为了地球,远离白色污染”的宣传活动,需要制定宣传单,选择社区附近的甲、乙两家印刷社印刷,他们各自制作这种宣传单的费用y(元)与宣传单数量x(张)之间的函数图象如图所示,结合图象解答下列问题:
(1)求甲印刷社制作这种宣传单每张的钱数.
(2)当x>500时,求乙印刷社所需的费用y与x之间的函数关系式.
(3)如果该社区在制作这种宣传单时,第一次印刷了800张宣传单,第二次印刷了1200张宣传单,直接写出该社区两次印刷这种宣传单共花费的最少钱数.
-
科目: 来源: 题型:
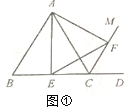
查看答案和解析>>【题目】【感知】如图①,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC中点,在CM上截取CF=BE,连接AE、EF、AF.易证:△AEF是等边三角形(不需要证明).
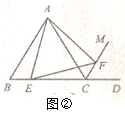
【探究】如图②,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC上一点(不与点B、C重合),在CM上截取CF=BE,连接AE、EF、AF.求证:△AEF是等边三角形.
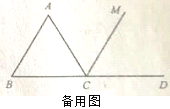
【应用】将图②中的“E是边BC上一点”改为“E是边BC延长线上一点”,其他条件不变.当四边形ACEF是轴对称图形,且AB=2时,请借助备用图,直接写出四边形ACEF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在数轴上点A,B所对应的数是-4,4.
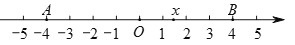
对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于-4,则称代数式N是线段AB的封闭代数式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的封闭代数式.
问题:
(1)关于x代数式|x-1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值和最小值分别是____ ______.
所以代数式|x-1|__________(填是或不是)线段AB的封闭代数式.
(2)以下关x的代数式:
①
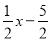 ;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.
;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.是线段AB的封闭代数式是__________,并证明(只需要证明是线段AB的封闭代数式的式子,不是的不需证明).
(
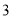 )关于x的代数式
)关于x的代数式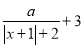 是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________.
是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知E、F、G、H分别是菱形ABCD的边AB、BC、CD、AD的中点,则四边形EFGH的形状一定是( )
A. 平行四边形B. 矩形C. 菱形D. 正方形
相关试题

