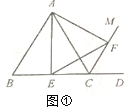
【题目】【感知】如图①,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC中点,在CM上截取CF=BE,连接AE、EF、AF.易证:△AEF是等边三角形(不需要证明).
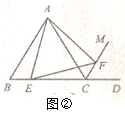
【探究】如图②,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC上一点(不与点B、C重合),在CM上截取CF=BE,连接AE、EF、AF.求证:△AEF是等边三角形.
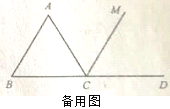
【应用】将图②中的“E是边BC上一点”改为“E是边BC延长线上一点”,其他条件不变.当四边形ACEF是轴对称图形,且AB=2时,请借助备用图,直接写出四边形ACEF的周长.
参考答案:
【答案】【探究】见解析;【应用】![]()
【解析】试题分析:【探究】根据等边三角形的性质和角平分线的性质证明△ABE≌△ACF,得到AE=AF,再证明∠EAF=60°,即可得到结论;
【应用】先证明△AEF为等边三角形,得到不可能以AE所在的直线为对称轴,只能以CF为对称轴,从而得到∠BAE=90°,以及AE的值,即可得到结论
试题解析:解:【探究】∵△ABC是等边三角形,∴AB=AC,∠B=∠ACB=60°,∴∠ACD=120°.∵CM是外角∠ACD的平分线,∴![]() ,∴∠B=∠ACF=60°.∵CF=BE,∴△ABE≌△ACF,∴AE=AF,∠BAE=∠CAF.∵∠BAC=60°,∴∠BAE+∠EAC=∠CAF +∠EAC,∴∠EAF=60°,∴△AEF是等边三角形.
,∴∠B=∠ACF=60°.∵CF=BE,∴△ABE≌△ACF,∴AE=AF,∠BAE=∠CAF.∵∠BAC=60°,∴∠BAE+∠EAC=∠CAF +∠EAC,∴∠EAF=60°,∴△AEF是等边三角形.
【应用】由题意得:△ABE≌△ACF,∴AE=AF,∠BAE=∠CAF,∴∠FAE=∠BAC=60°,∴△AEF为等边三角形,∴AE=AF=EF,∴不可能以AE所在的直线为对称轴,即以CF为对称轴.∵AB=2,∴AC=CE=2,∴AC=BC=CE,∴∠BAE=90°,∴AE=![]() ,∴四边形ACEF的周长为:
,∴四边形ACEF的周长为: ![]() =
=![]() .
.
-
科目: 来源: 题型:
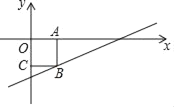
查看答案和解析>>【题目】如图所示,在第四象限内的矩形OABC,两边在坐标轴上,一个顶点在一次函数y=0.5x﹣3的图象上,当点A从左向右移动时,矩形的周长与面积也随之发生变化,设线段OA的长为m,矩形的周长为C,面积为S.
(1)试分别写出C、S与m的函数解析式,它们是否为一次函数?
(2)能否求出当m取何值时,矩形的周长最大?为什么?
-
科目: 来源: 题型:
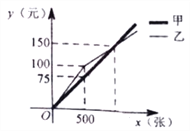
查看答案和解析>>【题目】某社区准备进行“为了地球,远离白色污染”的宣传活动,需要制定宣传单,选择社区附近的甲、乙两家印刷社印刷,他们各自制作这种宣传单的费用y(元)与宣传单数量x(张)之间的函数图象如图所示,结合图象解答下列问题:
(1)求甲印刷社制作这种宣传单每张的钱数.
(2)当x>500时,求乙印刷社所需的费用y与x之间的函数关系式.
(3)如果该社区在制作这种宣传单时,第一次印刷了800张宣传单,第二次印刷了1200张宣传单,直接写出该社区两次印刷这种宣传单共花费的最少钱数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径。
(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段AC,同时我们还发现损矩形中有公共边的两个三角形角的特点,在公共边的同侧的两个角是相等的。如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC。请再找一对这样的角来 =
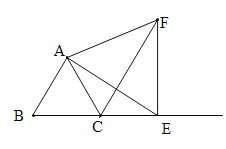
(2)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由。
(3)在第(2)题的条件下,若此时AB=
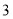 ,BD=
,BD=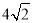 ,求BC的长。
,求BC的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在数轴上点A,B所对应的数是-4,4.
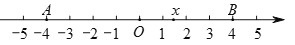
对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于-4,则称代数式N是线段AB的封闭代数式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的封闭代数式.
问题:
(1)关于x代数式|x-1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值和最小值分别是____ ______.
所以代数式|x-1|__________(填是或不是)线段AB的封闭代数式.
(2)以下关x的代数式:
①
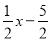 ;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.
;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.是线段AB的封闭代数式是__________,并证明(只需要证明是线段AB的封闭代数式的式子,不是的不需证明).
(
 )关于x的代数式
)关于x的代数式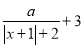 是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________.
是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知E、F、G、H分别是菱形ABCD的边AB、BC、CD、AD的中点,则四边形EFGH的形状一定是( )
A. 平行四边形B. 矩形C. 菱形D. 正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期
一
二
三
四
五
六
日
增减(辆)
-1
+3
-2
-4
+7
-5
-10
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
相关试题

