【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
(1)若AD=3![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE=![]() EF;
EF;
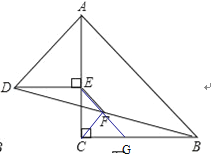
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.

参考答案:
【答案】(1)EF =2.5;(2)证明见解析;(3)(1)中的结论仍然成立.理由见解析.
【解析】试题分析:(1)等腰直角三角形的斜边长是直角边的![]() 倍,得到DE=3由于BE=4,利用勾股定理,得BD=5,再利用直角三角形斜边上的中线是斜边的一半,得以解决;
倍,得到DE=3由于BE=4,利用勾股定理,得BD=5,再利用直角三角形斜边上的中线是斜边的一半,得以解决;
(2)连接CF,需要证明![]() 是等腰直角三角形,根据四点共圆,得到点F是四边形DCBE的外接圆,且F是圆心,根据同弧所对的圆心角是圆周角的2倍,得
是等腰直角三角形,根据四点共圆,得到点F是四边形DCBE的外接圆,且F是圆心,根据同弧所对的圆心角是圆周角的2倍,得![]() 从而
从而![]() ,再根据直角三角形斜边上的中线是斜边的一半,得
,再根据直角三角形斜边上的中线是斜边的一半,得![]() ,得证
,得证![]() 是等腰直角三角形,结论得证;
是等腰直角三角形,结论得证;
(3)连接CF,延长EF交CB于点G,利用ASA证明△EDF≌△GBF,得出EF=GF,BG=DE=AE,进而证明CE=CG,得出△CEF为等腰直角三角形,利用三线合一证明![]() 结论得证。
结论得证。
试题解析:
(1)∵∠AED=90°,AE=DE,AD=3![]() ,
,
∴AE=DE=3,
在Rt△BDE中,
∵DE=3,BE=4,
∴BD=5,
又∵F是线段BD的中点,
∴EF=![]() BD=2.5;
BD=2.5;
(2)连接CF,线段CE与FE之间的数量关系是CE=![]() FE;
FE;
∵∠AED=∠ACB=90°
∴B、C、D、E四点共圆
且BD是该圆的直径,
∵点F是BD的中点,
∴点F是圆心,
∴EF=CF=FD=FB,
∴∠FCB=∠FBC,∠ECF=∠CEF,
由圆周角定理得:∠DCE=∠DBE,
∴∠FCB+∠DCE=∠FBC+∠DBE=45°
∴∠ECF=45°=∠CEF,
∴△CEF是等腰直角三角形,
∴CE=![]() EF.
EF.
(3)(1)中的结论仍然成立.
如图,连接CF,延长EF交CB于点G,
∵∠ACB=∠AED=90°,
∴DE∥BC,
∴∠EDF=∠GBF,
在△EDF和△GBF中,
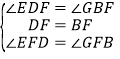 ,
,
∴△EDF≌△GBF,
∴EF=GF,BG=DE=AE,
∵AC=BC,
∴CE=CG,
∴∠EFC=90°,CF=EF,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴CE=![]() FE;
FE;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C,D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA的延长线与OC的延长线于点E,F,连接BF.

(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2019秒时,点P的坐标是________________
个单位长度,则第2019秒时,点P的坐标是________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊的毕达哥拉斯学派由古希腊哲学家毕达哥拉斯所创立,毕达哥拉斯学派认为数是万物的本原,事物的性质是由某种数量关系决定的,如他们研究各种多边形数:记第n个k边形数N(n,k)=
 n2+
n2+ n(n≥1,k≥3,k、n都为整数),
n(n≥1,k≥3,k、n都为整数),如第1个三角形数N(1,3)=
 ×12+
×12+ ×1=1;
×1=1;第2个三角形数N(2,3)=
 ×22+
×22+ ×2=3;
×2=3;第3个四边形数N(3,4)=
 ×32+
×32+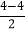 ×3=9;
×3=9;第4个四边形数N(4,4)=
 ×42+
×42+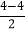 ×4=16.
×4=16.(1)N(5,3)=________,N(6,5)=________;
(2)若N(m,6)比N(m+2,4)大10,求m的值;
(3)若记y=N(6,t)-N(t,5),试求出y的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为(-2,-2),(3,1),(0,2),若把三角形ABC向上平移 3 个单位长度,再向左平移
 个单位长度得到三角形
个单位长度得到三角形  ,点A,B,C的对应点分别为
,点A,B,C的对应点分别为  ,
, ,
, .
.(1)写出点
 ,
, ,
, 的坐标;
的坐标;(2)在图中画出平移后的三角形
 ;
;(3)三角形
 的面积为__________.
的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四含五入”到个位的值记为
 ,即当n为非负整数时,若n-
,即当n为非负整数时,若n-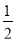 ≤x<n+
≤x<n+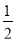 ,则
,则 =n.如:
=n.如: ,
, ,……根据以上材料,解决下列问题:
,……根据以上材料,解决下列问题:(1)填空
 = ,
= , = ;
= ;(2)若
 ,则x的取值范围是 ;
,则x的取值范围是 ;(3)求满足
 的所有实数x的值.
的所有实数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)如图,已知抛物线
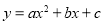 (
( )与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
相关试题

