【题目】如图:EF∥AD ,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整:

因为EF∥AD,所以∠2=__
又因为∠1=∠2,所以∠1=∠3
所以AB∥__
所以∠BAC+__=180°
因为∠BAC=70°,所以∠AGD=__
参考答案:
【答案】∠3 两直线平行,同位角相等
DG 内错角相等,两直线平行
∠AGD 110°
【解析】
根据平行线的性质和已知求出∠1=∠3,根据平行线的判定推出AB∥DG,根据平行线的性质求出∠BAC+∠DGA=180°即可.
∵EF∥AD
∴∠2=∠3(两直线平等,同位角相等)
又∵∠1=∠2
∴∠1=∠3(等量代换)
∴AB∥DG(内错角相等,两直线平等)
∴∠BAC+∠AGD=180°(两直线平等,同旁内角互补)
∵∠BAC=70°(已知)
∴∠AGD=180°-70°=110°(等量代换)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线相交于点O,点E,F,G,H分别是AO,BO,CO,DO的中点,请问四边形EFGH是矩形吗?请说明理由.
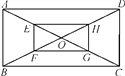
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD相交于点O,延长CB到点E,使BE=BC,连接AE.
(1)求证:四边形ADBE是平行四边形;
(2)若AB=4,OB=
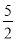 ,求四边形ADBE的周长.
,求四边形ADBE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
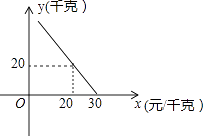
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知单位长度为1的方格中有三角形ABC.
(1)请画出三角形ABC向上平移3格再向右平移2格所得的三角形A′B′C′;
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标.

相关试题

