【题目】如图1,矩形ABCD中,AB=6,∠DBC=30°,DM平分∠BDC交BC于M,△EFG中,∠F=90°,GF= ![]() ,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒
,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒 ![]() 个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,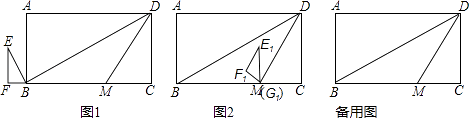
(1)当△E1F1G1的顶点G1恰好在BD上时,t=秒;
(2)直接写出S与t的函数关系式,及自变量t的取值范围;
(3)如图2,△E1F1G1平移到G1与M重合时,将△E1F1G1绕点M旋转α°(0°<α<180°)得到△E2F2G1 , 点E1、F1分别对应E2、F2 , 设直线F2E2与直线DM交于P,与直线DC交于Q,是否存在这样的α,使△DPQ为直角三角形?若存在,求α的度数和DQ的长;若不存在,请说明理由.
参考答案:
【答案】
(1)3
(2)
解:在Rt△DCM中,∵∠C=90°,CD=6,∠CDM=30°,
∴CM=2 ![]() ,DM=4
,DM=4 ![]() ,
,
∴BM=4 ![]() .
.
①如图2中,当0<t≤4时,重叠部分是四边形NF1GH,

S=S ![]() ﹣S
﹣S ![]() =
= ![]() ×3×
×3× ![]() ﹣
﹣ ![]() (2
(2 ![]() ﹣
﹣ ![]() t)(2﹣
t)(2﹣ ![]() t)=﹣
t)=﹣ ![]() t2+2
t2+2 ![]() t﹣
t﹣ ![]()
![]() ,
,
②如图3中,当4<t≤7时,重叠部分是四边形GHNF1,

S=S ![]() ﹣S
﹣S ![]() =
= ![]() ﹣
﹣ ![]() [2
[2 ![]() ﹣
﹣ ![]() (8
(8 ![]() ﹣
﹣ ![]() t)][2﹣
t)][2﹣ ![]() (8﹣t)]=﹣
(8﹣t)]=﹣ ![]() t2+
t2+ ![]() t﹣
t﹣ ![]() ,
,
③如图4中,当7<t≤8时,重叠部分是△GHN,

S= ![]()
![]() (8
(8 ![]() ﹣
﹣ ![]() t)
t) ![]() (8
(8 ![]() ﹣
﹣ ![]() t)=
t)= ![]() t2﹣6
t2﹣6 ![]() t+24
t+24 ![]() ,
,
综上所述,S= 
(3)
解:存在.
理由:①如图5中,当∠DQP=90°时,

∵∠QCM=∠CQF2=∠QF2M=90°,
∴四边形MCQF2是矩形,
∴CQ=MF2= ![]() ,∠F2MC=90°
,∠F2MC=90°
∴α=90°,DQ=CD﹣CQ=6= ![]() .
.
②如图6中,当∠DPQ=90°时,点P与点F2重合,点E、Q、C重合,此时α=120°,DQ=CD=6.

综上所述,当α=90°,DQ=6﹣ ![]() 或α=120°,DQ=6时,△DPQ为直角三角形
或α=120°,DQ=6时,△DPQ为直角三角形
【解析】解:(1)如图1中,连接AC交BD于点O,作OH⊥BC于点H.
∵四边形ABCD是矩形,
∴AB=CD=6,BO=OD,
∴BH=HC,
∴OH= ![]() CD=3,
CD=3,
在Rt△DBC中,∵CD=6,∠DBC=30°,
∴BC=6 ![]() ,BD=12,BH=HC=3
,BD=12,BH=HC=3 ![]()
∵在△EFG中,∠F=90°,GF= ![]() ,∠E=30°,
,∠E=30°,
∴EF=3,EB=2 ![]() ,
,
∴当△E1F1G1的顶点E1恰好在BD上时,点E平移到点O处.
此时t= ![]() =3,
=3,
∴t=3时,△E1F1G1的顶点E1恰好在BD上,
所以答案是3.
【考点精析】关于本题考查的翻折变换(折叠问题),需要了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.
-
科目: 来源: 题型:
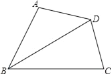
查看答案和解析>>【题目】如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
求证:∠A+∠C=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90°,BD是中线,AF⊥BD,F为垂足,过点C作AB的平行线交AF的延长线于点E.

求证:(1)∠ABD=∠FAD;(2)AB=2CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
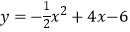 与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,
与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,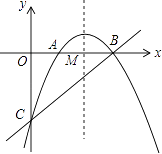
(1)求△ABC的面积;
(2)若p是x轴上方的抛物线上的一个动点,求点P到直线BC的距离的最大值;
(3)若点P在抛物线上运动(点P异于点A),当∠PCB=∠BCA时,求直线PC的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )

A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
-
科目: 来源: 题型:
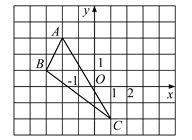
查看答案和解析>>【题目】(1)如图,在平面直角坐标系中,请画出△ABC关于y轴对称的△A′B′C′,并写出A′,B′,C′三点的坐标;(其中A′,B′,C′分别是A,B,C的对应点,不写画法)
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的
 :若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
:若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.6万元,乙队每天的施工费用为5.4万元,工程预算的施工费用为1000万元.若在甲、乙工程队工作效率不变的情况下使施工时间最短,问拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?
相关试题

