【题目】如图,在△ABC中,AB=AC,∠BAC=90°,BD是中线,AF⊥BD,F为垂足,过点C作AB的平行线交AF的延长线于点E.

求证:(1)∠ABD=∠FAD;(2)AB=2CE.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据同角的余角相等即可证明结论;(2)利用ASA证明△BAD≌△ACE,即可得AD=CE;再由AC=2AD=2CE即可得AB=2CE.
证明:(1)∵∠BAC=90°,
∴∠FAD+∠BAF=90°.
∵AF⊥BD,
∴在Rt△ABF中,∠ABD+∠BAF=90°,
∴∠ABD=∠FAD.
(2)∵CE∥AB,∠BAC=90°,∴∠ACE=90°,
在△BAD和△ACE中,
∵∠ABD=∠CAE,AB=CA,∠BAC=∠ACE=90°,
∴△BAD≌△ACE(ASA),
∴AD=CE.
∵BD为△ABC中AC边上的中线.
∴AC=2AD,
∴AC=2CE.
又∵AB=AC,
∴AB=2CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在出行中,主动采用能降低二氧化碳排放量的交通方式,谓之“低碳出行”.明明一家积极响应政府“绿色山城,低碳出行”的号召,今年2月﹣5月明明一家减少了驾车出行,他们将2月﹣5月驾车行驶的里程统计后绘制成以下两幅不完整的统计图:
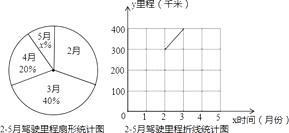
(1)扇形统计图中x= , 并补全折线统计图;
(2)某中学也积极参与“绿色山城,低碳出行”活动中,决定从4名广播社骨干成员中(其中两名男生,两名女生)选拔两名同学去演讲宣传,请用画树形图或列表的方法求所选出的两名同学恰好是一名男生一名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:

(1)EH=FH;
(2)∠CAB=2∠CDH. -
科目: 来源: 题型:
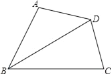
查看答案和解析>>【题目】如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
求证:∠A+∠C=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
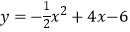 与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,
与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,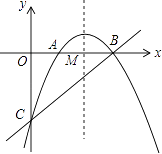
(1)求△ABC的面积;
(2)若p是x轴上方的抛物线上的一个动点,求点P到直线BC的距离的最大值;
(3)若点P在抛物线上运动(点P异于点A),当∠PCB=∠BCA时,求直线PC的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD中,AB=6,∠DBC=30°,DM平分∠BDC交BC于M,△EFG中,∠F=90°,GF=
 ,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒
,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒  个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,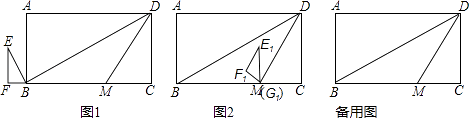
(1)当△E1F1G1的顶点G1恰好在BD上时,t=秒;
(2)直接写出S与t的函数关系式,及自变量t的取值范围;
(3)如图2,△E1F1G1平移到G1与M重合时,将△E1F1G1绕点M旋转α°(0°<α<180°)得到△E2F2G1 , 点E1、F1分别对应E2、F2 , 设直线F2E2与直线DM交于P,与直线DC交于Q,是否存在这样的α,使△DPQ为直角三角形?若存在,求α的度数和DQ的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )

A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
相关试题

