Question

【题目】如图，△ABC的两条角平分线BD、CE交于O，且∠A=60°，则下列结论中不正确的是（ ）

A．∠BOC=120° B．BC=BE+CD C．OD=OE D．OB=OC

Answer 1

【答案】D

【解析】

试题分析：根据三角形的内角和等于180°求出∠ABC+∠ACB=120°，再根据角平分线的性质求出∠OBC+∠OCB=60°，然后利用三角形的内角和等于180°列式计算即可求出∠BOC的度数；

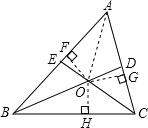
连接OA，作OF⊥AB于点F，OG⊥AC于点G，OH⊥BC于点H，根据角平分线上的点到角的两边的距离相等可得OF=OG=OH，从而可得△BOF和△BOH全等，△COG和△COH全等，根据全等三角形对应边相等可得BH=BF，CH=CG，再根据四边形的内角和求出∠FOG=120°，根据对顶角相等求出∠EOD=120°，然后推出∠EOF=∠DOG，再利用“角边角”证明△EOF和△DOG全等，根据全等三角形对应边相等可得EF=DG，OD=OE，即可判定出B、C选项都正确，根据等角对等边的性质，只有∠ABC=∠ACB时才能得到OB=OC，所以D选项错误．

解：∵∠A=60°，

∴∠ABC+∠ACB=180°﹣∠A=180°﹣60°=120°，

∵△ABC的两条角平分线BD、CE交于O，

∴∠OBC=∠ABC，∠OCB=∠ACB，

∴∠BOC=180°﹣（∠OBC+∠OCB）=180°﹣（∠ABC+∠ACB）=120°，故A选项正确；

如图，连接OA，作OF⊥AB于点F，OG⊥AC于点G，OH⊥BC于点H，

∵△ABC的两条角平分线BD、CE交于O，

∴OF=OG=OH，

利用“HL”可得△BOF≌△BOH，△COG≌△COH，

∴BH=BF，CH=CG，

在四边形AFOG中，∠FOG=360°﹣60°﹣90°×2=120°，

∴DOG=∠FOG﹣∠DOF=120°﹣∠DOF，

又∵∠EOD=∠BOC=120°，

∴∠EOF=∠EOD﹣∠DOF=120°﹣∠DOF，

∴∠EOF=∠DOG，

在△EOF和△DOG中，，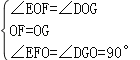

∴△EOF≌△DOG（ASA），

∴EF=DG，OD=OE，故C选项正确；

∴BC=BH+CH=BF+CG=BE+EF+CD﹣DG=BE+CD，

即BC=BE+CD，故B选项正确；

只有当∠ABC=∠ACB时，∵△ABC的两条角平分线BD、CE交于O，

∴∠OBC=∠ABC，∠OCB=∠ACB，

∴∠OBC=∠OCB，

∴OB=OC，

而本题无法得到∠ABC=∠ACB，

所以，OB=OC不正确，故D选项错误．

故选D．