【题目】如图1,直线![]() ,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP, 连结PQ,设点P的坐标为P(0,t).
,与x轴、y轴分别交于点A、C,以AC为对角线作矩形OABC,点P、Q分别为射线OC、射线AC上的动点,且有AQ=2CP, 连结PQ,设点P的坐标为P(0,t).
(1)求点B的坐标.
(2)若t=1时,连接BQ,求△ABQ的面积.
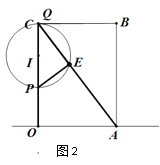
(3)如图2,以PQ为直径作⊙I,记⊙I与射线AC的另一个交点为E.
① 若![]() ,求此时t的值.
,求此时t的值.
② 若圆心I在△ABC内部(不包含边上),则此时t的取值范围为 .(直接写出答案)
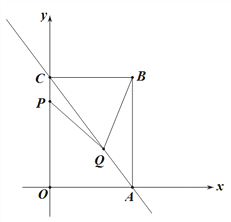
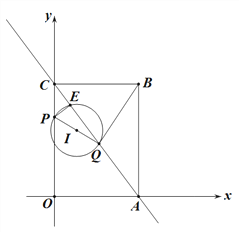
图1 图2
参考答案:
【答案】(1)B(6,8);(2)![]() ;(3)①
;(3)①![]() ,
, ![]() ,
, ![]() ,
, ![]() ;②
;②![]()
【解析】(1)解:将x=0代入![]() ,得y=8,∴C(0,8)
,得y=8,∴C(0,8)
将y=0代入![]() ,得x=6 ∴A(6,0)
,得x=6 ∴A(6,0)
∵矩形OABC ∴B(6,8)
(2) 作QH⊥AB于H,当t=1时,CP=7,AQ=14
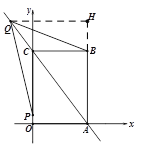
易证AC=10, sin∠BAC=![]() ,
,
∴QH=AQsin∠BAC=![]()
∴S△ABQ=![]()
(3)分类:① 当P在线段OC上,Q在线段AC上时,即3<<8时,
如图1,易证![]() =sin∠EQP=sin∠ACO=
=sin∠EQP=sin∠ACO=![]() ,∴∠EQP=∠ACO∴CP=PQ
,∴∠EQP=∠ACO∴CP=PQ
∵PE⊥CQ,∴CE=EQ∴![]() 解得
解得![]()
②当Q与C重合,P在OC上时,如图2,可得16-2t=10,解得![]()
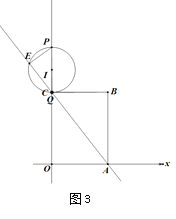
③当Q与C重合,P在OC延长线上时,如图3,可得2t-16=10,解得![]()
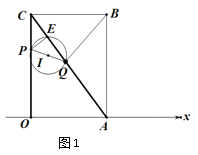
④当P在OC延长线上,Q在AC延长线上时,如图4,同①,可得∠Q=∠PCQ
∴CP=PQ∴![]() , 解得
, 解得![]()
∴![]()
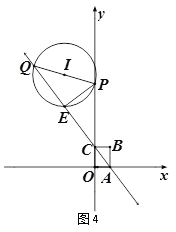
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】王大伯有甲、乙、丙三块不同等级的棉田60亩、20亩、10亩,想估算自己今年的棉花产量,请你给王大伯出个主意( )
A.从甲棉田抽出部分进行估算
B.从乙棉田抽出部分进行估算
C.从丙棉田抽出部分进行估算
D.按6:2:1的比例从甲、乙、丙三块棉田抽取进行估算 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】要想统计“本班学生最喜欢的动画片”,下列收集数据的方法比较合适的是( )
A.调查问卷
B.访问
C.观察
D.查阅资料 -
科目: 来源: 题型:
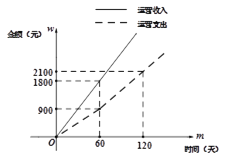
查看答案和解析>>【题目】环保健康的“共享单车”已成为人们短途出行的一种新方式,一辆新投放市场的单车其先期成本为1050元. 如图是一辆新投放的共享单车其运营收入
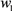 和运营支出
和运营支出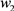 关于时间
关于时间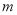 的函数图象。
的函数图象。注:一辆单车的盈利=运营收入-运营支出-先期成本
(1)分别求
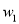 及运营60天后
及运营60天后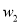 关于时间
关于时间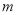 的函数关系式.
的函数关系式.(2)求一辆新投放市场的单车恰好收回先期成本需要运营多少天?
(3)某公司投放市场一批单车,其先期成本不少于2.1万元但不超过10.5万元,经过一段时间的市场试运营共盈利3550元,则该公司试运营的天数为 天(直接写出答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】沿着x轴正方向看,抛物线y=﹣(x﹣1)2在对称轴_____侧的部分是下降的(填“左”、“右”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数的图象经过点(4,﹣3),且当x=3时,有最大值﹣1,则该二次函数解析式为_____.
相关试题

