【题目】(题型一)请你参与下面的探究过程,完成所提出的问题.
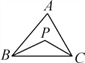
(1)探究1:如图11-3-3(1),P是△ ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70°,求∠BPC度数.
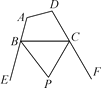
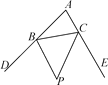
(2)探究2:如图11-3-3(2),P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系,并说明理由.边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.
①直接写出∠BPC与α的数量关系;
②根据α值的情况,判断△BPC的形状.(按角分类)
(1) (2) (3)
参考答案:
【答案】(1)∠BPC=125°;
(2)∠BPC=90°-![]() ∠A.理由见解析;
∠A.理由见解析;
(3)当0°<α<180°时,△BPC是钝角三角形;当α=180°时,△BPC是直角三角形;当α>180°时,△BPC是锐角三角形.
【解析】试题分析:(1)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再根据角平分线的性质求出∠PBC+∠BCP的度数,由三角形内角和定理即可求出答案;
(2)根据角平分线的定义可得∠PCE=![]() ∠BCE,∠PBD=
∠BCE,∠PBD=![]() ∠CBD,然后根据三角形内角和定理列式整理即可得解;
∠CBD,然后根据三角形内角和定理列式整理即可得解;
(3)①根据四边形的内角和定理表示出∠BAD+∠CDA,然后同理(2)解答即可;②根据α的值的情况,得到∠P的取值范围,即可得到结论.
试题解析:(1)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°.
∵BP,CP分别是∠ABC,∠ACB的平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∴∠PBC+∠BCP=1/2(∠ABC+∠ACB)=55°.
∵∠PBC+∠BCP+∠BPC=180°,
∴∠BPC=125°.
(2)∠BPC=90°-![]() ∠A.
∠A.
理由:∵BP,CP分别是外角∠DBC,∠ECB的平分线,
∴∠PBC+∠PCB=![]() (∠DBC+∠ECB)=
(∠DBC+∠ECB)=![]() (180°+∠A).
(180°+∠A).
在△PBC中,∠BPC=180°-![]() (180°+∠A)=90°-
(180°+∠A)=90°-![]() ∠A.
∠A.
(3)如图,
①延长BA,CD交于点Q,
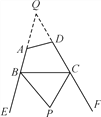
由(2)可知,∠BPC=90°-![]() ∠Q,
∠Q,
∴∠Q=180°-2∠BPC,
∴∠BAD+∠CDA=180°+∠Q=180°+180°-2∠BPC=360°-2∠BPC.
∴∠BPC=180°-![]() α.
α.
②当0°<α<180°时,△BPC是钝角三角形;
当α=180°时,△BPC是直角三角形;
当α>180°时,△BPC是锐角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学知道自己的成绩后,要判断能否进入决赛,还需知道这9名同学成绩的( )
A. 众数B. 中位数C. 平均数D. 方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】把函数y=﹣2x+3的图象向下平移4个单位后的函数图象的解析式为( )
A.y=﹣2x+7B.y=﹣6x+3C.y=﹣2x﹣1D.y=﹣2x﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)-24; (2)
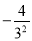 ; (3)-(-
; (3)-(-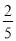 )3;
)3;(4)32÷(-2)3; (5)-12-(-1)2; (6)(-2)2-23-(-2)3-24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四个数:-2,-3,4,-1,任取其中两个数相乘,所得的积的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.
(1)补全条形统计图.
(2)若全校共有3600位学生家长,据此估计,有多少位家长最关心孩子“情感品质”方面的成长?
(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和指导?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D,E分别是△ABC边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=α.(注:四边形的内角和是360°)
(1)若点P在线段AB上,如图11-2-13(1),且α=50°,则∠1+∠2= .
(2)若点P在边AB上运动,如图11-2-13(2),则α,∠1,∠2之间的关系为 .
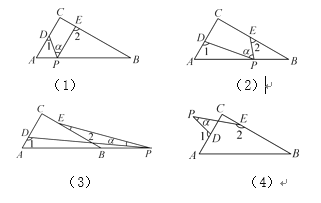
(3)若点P运动到边AB的延长线上,图11-2-13(3),则α,∠1,∠2之间有何关系?请写出你的猜想,并说明理由.
(4)若点P运动到△ABC外,如图11-2-13(4),则α,∠1,∠2之间的关系为 .
相关试题

