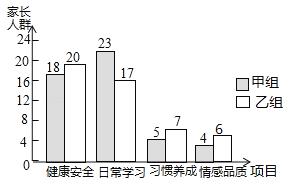
【题目】为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.
(1)补全条形统计图.
(2)若全校共有3600位学生家长,据此估计,有多少位家长最关心孩子“情感品质”方面的成长?
(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和指导?

参考答案:
【答案】(1)答案见解析;(2)360;(3)答案不唯一.
【解析】
试题分析:(1)用甲、乙两班学生家长共100人减去其余各项目人数可得乙组关心“情感品质”的家长人数,补全图形即可;
(2)用样本中关心孩子“情感品质”方面的家长数占被调查人数的比例乘以总人数3600可得答案;
(3)无确切答案,结合自身情况或条形统计图,言之有理即可.
试题解析:(1)乙组关心“情感品质”的家长有:100﹣(18+20+23+17+5+7+4)=6(人),补全条形统计图如图:
(2)![]() ×3600=360(人).
×3600=360(人).
答:估计约有360位家长最关心孩子“情感品质”方面的成长;
(3)无确切答案,结合自身情况或条形统计图,言之有理即可,如:从条形统计图中,家长对“情感品质”关心不够,可适当关注与指导.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)-24; (2)
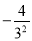 ; (3)-(-
; (3)-(-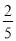 )3;
)3;(4)32÷(-2)3; (5)-12-(-1)2; (6)(-2)2-23-(-2)3-24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题型一)请你参与下面的探究过程,完成所提出的问题.
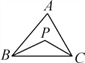
(1)探究1:如图11-3-3(1),P是△ ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70°,求∠BPC度数.
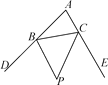
(2)探究2:如图11-3-3(2),P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系,并说明理由.边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.
①直接写出∠BPC与α的数量关系;
②根据α值的情况,判断△BPC的形状.(按角分类)
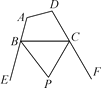
(1) (2) (3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四个数:-2,-3,4,-1,任取其中两个数相乘,所得的积的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D,E分别是△ABC边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=α.(注:四边形的内角和是360°)
(1)若点P在线段AB上,如图11-2-13(1),且α=50°,则∠1+∠2= .
(2)若点P在边AB上运动,如图11-2-13(2),则α,∠1,∠2之间的关系为 .
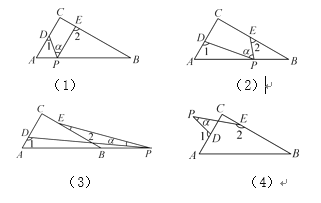
(3)若点P运动到边AB的延长线上,图11-2-13(3),则α,∠1,∠2之间有何关系?请写出你的猜想,并说明理由.
(4)若点P运动到△ABC外,如图11-2-13(4),则α,∠1,∠2之间的关系为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算-1-2×(-3)的结果等于( )
A. 5 B. -5 C. 7 D. -7
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(-10)×(-8.24)×(-0.1)=________.
相关试题

