【题目】如图,在Rt△ABC中,∠C=90°,点D,E分别是△ABC边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=α.(注:四边形的内角和是360°)
(1)若点P在线段AB上,如图11-2-13(1),且α=50°,则∠1+∠2= .
(2)若点P在边AB上运动,如图11-2-13(2),则α,∠1,∠2之间的关系为 .
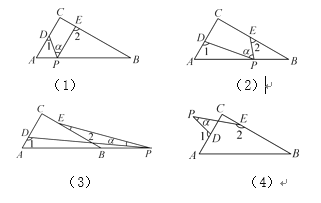
(3)若点P运动到边AB的延长线上,图11-2-13(3),则α,∠1,∠2之间有何关系?请写出你的猜想,并说明理由.
(4)若点P运动到△ABC外,如图11-2-13(4),则α,∠1,∠2之间的关系为 .
参考答案:
【答案】(1)140°;(2)∠1+∠2=90°+α;(3)∠1=90°+∠2+α.理由见解析;(4)∠2=90°+∠1-α.
【解析】(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+α.
∵∠C=90°,α=50°,
∴∠1+∠2=140°.
(2)由(1)得α+∠C=∠1+∠2,
∴∠1+∠2=90°+α.
(3)∠1=90°+∠2+α.
理由如下:
如图D11-2-6(1),∵∠2+α=∠DME,∠DME+∠C=∠1,∴∠1=∠C+∠2+α=90°+∠2+α.
(4)如图D11-2-6(2),∵∠PFC=∠DFE,∴α+180°-∠1=∠C+180°-∠2,
∴∠2=90°+∠1-α.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(题型一)请你参与下面的探究过程,完成所提出的问题.
(1)探究1:如图11-3-3(1),P是△ ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70°,求∠BPC度数.
(2)探究2:如图11-3-3(2),P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系,并说明理由.边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.
①直接写出∠BPC与α的数量关系;
②根据α值的情况,判断△BPC的形状.(按角分类)
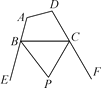
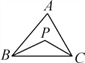
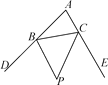
(1) (2) (3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四个数:-2,-3,4,-1,任取其中两个数相乘,所得的积的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.
(1)补全条形统计图.
(2)若全校共有3600位学生家长,据此估计,有多少位家长最关心孩子“情感品质”方面的成长?
(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和指导?

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算-1-2×(-3)的结果等于( )
A. 5 B. -5 C. 7 D. -7
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(-10)×(-8.24)×(-0.1)=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
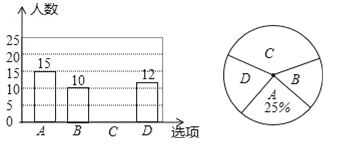
请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)若该学校共有3600名学生,试估计该校最想去湿地公园的学生人数.
相关试题

