【题目】如图,矩形ABCD中,AD=2AB,E、F、G、H分别是AB,BC,CD,AD边上的点,EG⊥FH,FH=2 ![]() ,则四边形EFGH的面积为( )
,则四边形EFGH的面积为( ) 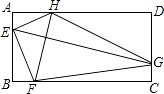
A.8 ![]()
B.8
C.12 ![]()
D.24
参考答案:
【答案】B
【解析】解:过F作FM⊥AD于M,过E作EN⊥CD于N,EN与MF交于点Z, 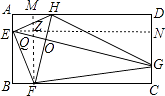
则∠FMH=∠ENG=90°,
∵四边形ABCD是矩形,EG⊥FH,
∴∠A=∠D=∠AEN=∠EOF=∠EZF=90°,
∴四边形AEND是矩形,
∴AD=EN,
同理AB=FM,
∵AD=2AB,
∴EN=2FM,
∵∠NEG+∠EQZ+∠EZQ=180°,∠MFH+∠EOF+∠FQO=180°,∠EQZ=∠FQO,
∴∠MFH=∠NEG,
∵∠FMH=∠ENG=90°,
∴△FMH∽△ENG,
∴ ![]() =2,
=2,
∵FH=2 ![]() ,
,
∴EG=4 ![]() ,
,
∴ ![]() EGπEG×FH=
EGπEG×FH= ![]() ×2
×2 ![]() ×4
×4 ![]() =8,
=8,
故选:B.
过F作FM⊥AD于M,过E作EN⊥CD于N,根据矩形的性质和判定推出EN=2FH,求出EN的长,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABM=37°,AB=20,C是射线BM上一点.
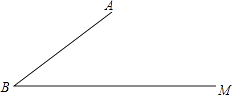
(1)求点A到BM的距离;
(2)在下列条件中,可以唯一确定BC长的是;(填写所有符合条件的序号)
①AC=13;②tan∠ACB= ;③连接AC,△ABC的面积为126.
;③连接AC,△ABC的面积为126.
(3)在(2)的答案中,选择一个作为条件,画出草图,求BC.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75) -
科目: 来源: 题型:
查看答案和解析>>【题目】先让我们一起来学习方程m2+1=
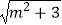 的解法:
的解法:
解:令m2=a,则a+1= ,方程两边平方可得,(a+1)2=a+3
,方程两边平方可得,(a+1)2=a+3
解得a1=1,a2=﹣2,∵m2≥0∴m2=1∴m=±1
点评:类似的方程可以用“整体换元”的思想解决.
不妨一试:
如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
(1)求抛物线的解析式;
(2)①当P点运动到A点处时,通过计算发现:POPH(填“>”、“<”或“=”);
(3)当△PHO为等边三角形时,求点P坐标;
(4)如图2,设点C(1,﹣2),问是否存在点P,使得以P、O、H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某同学在沙滩上用石子摆成的小房子.观察图形的变化规律,第6个小房子用的石子数量为 ( )

A. 87 B. 77 C. 70 D. 60
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)比较大小;
①|﹣2|+|3| |﹣2+3|;
②|4|+|3| |4+3|;
③|﹣
 |+|﹣
|+|﹣ | |﹣
| |﹣ +(﹣
+(﹣ )|;
)|;④|﹣5|+|0| |﹣5+0|.
(2)通过(1)中的大小比较,猜想并归纳出|a|+|b|与|a+b|的大小关系,并说明a,b满足什么关系时,|a|+|b|=|a+b|成立?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有三个有理数a,b,c,已知a=
 ,(n为正整数)且a与b互为相反数,b与c互为倒数.
,(n为正整数)且a与b互为相反数,b与c互为倒数.(1)当n为奇数时你能求出a,b,c各是几吗?
(2)当n为偶数时,你能求a,b,c三数吗?若能请算出结果,不能请说明理由.
(3)根据(1)中的结论,求:ab﹣b﹣(b﹣c)2015的值.
相关试题

