搜索
【题目】如图，已知∠ABM=37°，AB=20，C是射线BM上一点．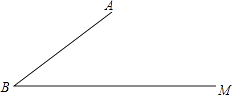
（1）求点A到BM的距离；
（2）在下列条件中，可以唯一确定BC长的是；（填写所有符合条件的序号）
①AC=13；②tan∠ACB= 
；③连接AC，△ABC的面积为126．
（3）在（2）的答案中，选择一个作为条件，画出草图，求BC．
（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）
参考答案：
【答案】
（1）
解：作AD⊥BC于D，则∠ADB=90°．
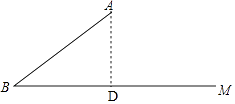
在Rt△ABD中，∵∠ADB=90°，
∴AD=ABsinB=12
（2）②③
（3）
解：方案一：选②，
由（1）得，AD=12，BD=ABcosB=16，
在Rt△ACD中，∵∠ADC=90°，
∴CD= 
=5，
∴BC=BD+CD=21．
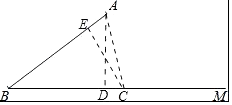
方案二：选③，
作CE⊥AB于E，则∠BEC=90°，
由S△ABC= 
ABCE得CE=12.6，
在Rt△BEC中，
∵∠BEC=90°，
∴BC= 
=21
【解析】解： （2）①以点A为圆心、13为半径画圆，与BM有两个交点，不唯一；
②由tan∠ACB= 
知∠ACB的大小确定，在△ABC中，∠ACB、∠B及AB确定，此时的三角形唯一；
③AB的长度和三角形的面积均确定，则点C到AC的距离即可确定，则BM上的点C是唯一的；
所以答案是：②③；
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在纸面上有一数轴（如图），折叠纸面．例如：若数轴上数2表示的点与数﹣2表示的点重合，则数轴上数﹣4表示的点与数4表示的点重合，根据你对例题的理解，解答下列问题：
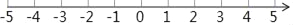
若数轴上数﹣3表示的点与数1表示的点重合．（根据此情境解决下列问题）
①则数轴上数3表示的点与数 表示的点重合．
②若点A到原点的距离是5个单位长度，并且A、B两点经折叠后重合，则B点表示的数是 ．
③若数轴上M、N两点之间的距离为2018，并且M、N两点经折叠后重合，
如果M点表示的数比N点表示的数大，则M点表示的数是 ．则N点表示的数是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=BC，以AB为直径的⊙O与AC交于点D，过点D作DF⊥BC，交AB的延长线于E，垂足为F．
（1）如图①，求证直线DE是⊙O的切线；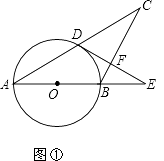
（2）如图②，作DG⊥AB于H，交⊙O于G，若AB=5，AC=8，求DG的长．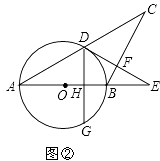
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2．
（1）点B在点A右边距A点4个单位长度，求点B所对应的数；
（2）在（1）的条件下，点A以每秒2个单位长度沿数轴向左运动，点 B 以每秒2个单位长度沿数轴向右运动，当点A运动到﹣6所在的点处时，求A，B两点间距离．
（3）在（2）的条件下，现A点静止不动，B点再以每秒2个单位长度沿数轴向左运动时，经过多长时间A，B两点相距4个单位长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先让我们一起来学习方程m2+1=
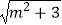的解法：
解：令m2=a，则a+1=
，方程两边平方可得，（a+1）2=a+3
解得a1=1，a2=﹣2，∵m2≥0∴m2=1∴m=±1
点评：类似的方程可以用“整体换元”的思想解决．
不妨一试：
如图1，在平面直角坐标系xOy中，抛物线y=ax2+1经过点A（4，﹣3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．
（1）求抛物线的解析式；
（2）①当P点运动到A点处时，通过计算发现：POPH（填“＞”、“＜”或“=”）；
（3）当△PHO为等边三角形时，求点P坐标；
（4）如图2，设点C（1，﹣2），问是否存在点P，使得以P、O、H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】下图是某同学在沙滩上用石子摆成的小房子．观察图形的变化规律，第6个小房子用的石子数量为 ( )
A. 87 B. 77 C. 70 D. 60
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AD=2AB，E、F、G、H分别是AB，BC，CD，AD边上的点，EG⊥FH，FH=2
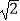，则四边形EFGH的面积为（ ）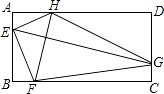 
A.8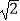
B.8
C.12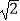
D.24
相关试题
