【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA= , PC=;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由. 
参考答案:
【答案】
(1)t;34﹣t
(2)解:当P点在Q点右侧,且Q点还没有追上P点时,
3t+2=14+t
解得:t=6,
∴此时点P表示的数为﹣4,
当P点在Q点左侧,且Q点追上P点后,相距2个单位,
3t﹣2=14+t解得:t=8,
∴此时点P表示的数为﹣2,
当Q点到达C点后,当P点在Q点左侧时,
14+t+2+3t﹣34=34
解得:t=13,
∴此时点P表示的数为3,
当Q点到达C点后,当P点在Q点右侧时,
14+t﹣2+3t﹣34=34
解得:t=14,
∴此时点P表示的数为4,
综上所述:点P表示的数为﹣4,﹣2,3,4
【解析】解:(1)∵动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒,
∴P到点A的距离为:PA=t,P到点C的距离为:PC=(24+10)﹣t=34﹣t;
所以答案是:t,34﹣t;
【考点精析】掌握数轴和两点间的距离是解答本题的根本,需要知道数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣3)2+(﹣4)0=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校规定学生的学期体育成绩有三部分组成:早锻炼及体育课外活动占10%,体育理论测试占30%,体育技能占60%.王明的三项成绩依次为90分,85分,90分,则王明学期的体育成绩是分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB等于( )
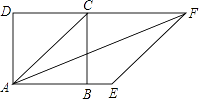
A.22.5°
B.45°
C.30°
D.135° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图AB∥CD,∠1=∠2,EP⊥FP,则以下错误的是( )
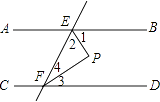
A.∠3=∠4
B.∠2+∠4=90°
C.∠1与∠3互余
D.∠1=∠3 -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b在数轴上的对应点的位置如图所示,则下列式子中正确的是( )

①b<0<a;②|b|<|a|;③ab>0;④a-b>a+b。
A.①②
B.①④
C.②③
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(﹣2,0),(﹣1,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标是 .
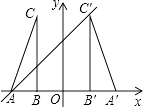
相关试题

