【题目】如图,在![]() 中,
中,![]() ,
,![]() ,如图:(1)以
,如图:(1)以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 、
、![]() 于点
于点![]() 和
和![]() ;(2)分别以
;(2)分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ;(3)连结
;(3)连结![]() 并延长交
并延长交![]() 于点
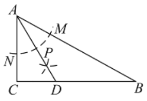
于点![]() .根据以上作图过程,下列结论中错误的是( )
.根据以上作图过程,下列结论中错误的是( )
A.![]() 是
是![]() 的平分线B.
的平分线B.![]()
C.点![]() 在
在![]() 的中垂线上D.
的中垂线上D.![]()
参考答案:
【答案】D
【解析】
根据作图的过程可以判定AD是∠BAC的角平分线;利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三线合一”的性质可以证明点D在AB的中垂线上;利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.
解:A、根据作图方法可得AD是∠BAC的平分线,正确;
B、∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=30°,
∴∠ADC=60°,正确;
C、∵∠B=30°,∠DAB=30°,
∴AD=DB,
∴点D在AB的中垂线上,正确;
D、∵∠CAD=30°,
∴CD=![]() AD,
AD,
∵AD=DB,
∴CD=![]() DB,
DB,
∴CD=![]() CB,
CB,
S△ACD=![]() CDAC,S△ACB=
CDAC,S△ACB=![]() CBAC,
CBAC,
∴S△ACD:S△ACB=1:3,
∴S△DAC:S△ABD≠1:3,错误,
故选:D.
-
科目: 来源: 题型:
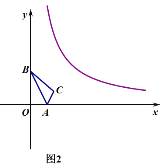
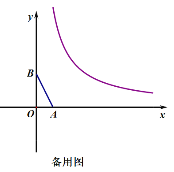
查看答案和解析>>【题目】已知:如图1,点A (1, 0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′ 恰在反比例函数y=
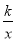 (x>0)的图象上.
(x>0)的图象上.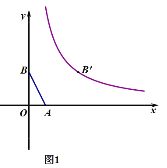
(1)求k的值;
(2)如图2,将△AOB (点O为坐标原点)沿AB翻折得到△ACB,求点C的坐标;
(3)是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF (即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=
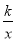 (x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
(x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
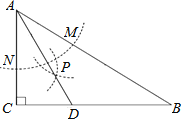
查看答案和解析>>【题目】(1)如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F.
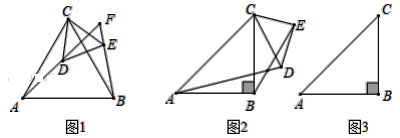
①求证:AD=BE;
②求∠AFB的度数.
(2)如图2,△ABC和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,直线AD和直线BE交于点F.
①求证:AD=
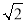 BE;
BE;②若AB=BC=3,DE=EC=
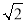 .将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度.
.将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,抛物线y=ax2+bx+c (a≠0)的顶点为M (1,9), 经过抛物线上的两点A(-3,-7)和B (3, m)的直线交抛物线的对称轴于点C.

(1)求抛物线的解析式和直线AB的解析式;
(2)在抛物线上是否存在点D,使得S△DAC=2S△DCM?若存在,求出点D的坐标;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点A、M、P、Q为顶点的四边形是平行四边形时,直接写出满足足条件的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:
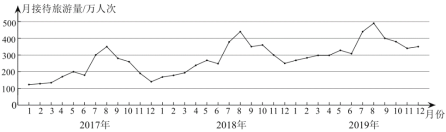
根据统计图提供的信息,下列推断不合理的是( )
A.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份
B.2019年的月接待旅游量的平均值超过300万人次
C.2017年至2019年,年接待旅游量逐年增加
D.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有红、黑两种颜色的球共60只,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,七(2)班的数学学习小组做了摸球实验.他们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到表中的一组统计数据:
摸球的次数n
50
100
300
500
800
1000
摸到红球的次数m
14
33
95
155
241
298
摸到红球的频率

0.28
0.33
0.317
0.31
0.301
0.298
请估计:当次数n足够大时,摸到红球的频率将会接近_____.(精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一组数据
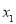 ,
,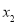 ,
,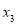 ,
,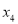 ,
,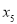 的方差是1,那么数
的方差是1,那么数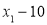 ,
,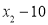 ,
,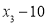 ,
,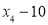 ,
,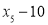 的方差是______.
的方差是______.
相关试题

