【题目】(1)已知关于x的方程x2+2mx+m2﹣1=0一个根为3,求m的值.
(2)已知α是锐角,且sin(α+15°)=![]() ,计算:
,计算:![]() ﹣4cosα﹣(π﹣3.14)0+tanα+(
﹣4cosα﹣(π﹣3.14)0+tanα+(![]() )﹣1的值.
)﹣1的值.
参考答案:
【答案】(1)m=﹣4或m=﹣2;(2)3
【解析】
试题分析:(1)把x=3代入方程计算即可求出m的值;
(2)由已知等式,利用特殊角的三角函数值求出α的度数,代入原式计算即可得到结果.
解:(1)∵x2+2mx+m2﹣1=0有一个根是3,
∴把x=3代入方程得:32+2m×3+m2﹣1=0,
整理得:m2+6m+8=0,
解得:m=﹣4或m=﹣2;
(2)∵sin60°=![]() ,
,
∴α+15°=60°,
∴α=45°,
则原式=2![]() ﹣4×
﹣4×![]() ﹣1+1+3=3.
﹣1+1+3=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条不同的直线a,b,c在同一平面内,下列命题中:
①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题有__________.(填写真命题的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).根据上述信息,解答下列各题:
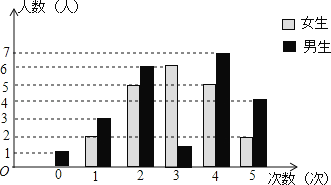
(1)该班级女生人数是 ;女生收看“两会”新闻次数的众数是 ;中位数是 .
(2)求女生收看次数的平均数.
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明计算出女生收看“两会”新闻次数的方差为
 ,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.(4)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”,如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )

A. 2 B. 3 C. 1 D. 8
-
科目: 来源: 题型:
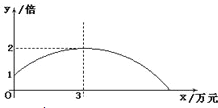
查看答案和解析>>【题目】某公司销售一种产品,每件产品的成本价、销售价及月销售量如表;为了获取更大的利润,公司决定投入一定的资金做促销广告,结果发现:每月投入的广告费为x万元,产品的月销售量是原销售量的y倍,且y与x的函数图象为如图所示的一段抛物线.
成本价(元/件)
销售价(元/件)
销售量(万件/月)
2
3
9
(1)求y与x的函数关系式为 ,自变量x的取值范围为 ;
(2)已知利润等于销售总额减去成本费和广告费,要使每月销售利润最大,问公司应投入多少广告费?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
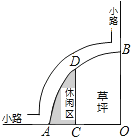
A.(10π﹣
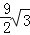 )米2 B.(π﹣
)米2 B.(π﹣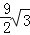 )米2
)米2 C.(6π﹣
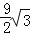 )米2 D.(6π﹣
)米2 D.(6π﹣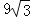 )米2
)米2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
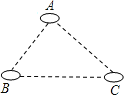
A.在AC,BC两边高线的交点处
B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处
D.在∠A,∠B两内角平分线的交点处
相关试题

