【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)如图1,当tan∠PAB=1,c=4 ![]() 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
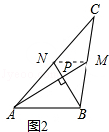
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
参考答案:
【答案】
(1)4 ![]() ;4
;4 ![]() ;
;![]()
;![]()
(2)
结论a2+b2=5c2.
证明:如图3中,连接MN.
∵AM、BN是中线,
∴MN∥AB,MN= ![]() AB,
AB,
∴△MPN∽△APB,
∴ ![]() =
= ![]() =
= ![]() ,
,
设MP=x,NP=y,则AP=2x,BP=2y,
∴a2=BC2=4BM2=4(MP2+BP2)=4x2+16y2,
b2=AC2=4AN2=4(PN2+AP2)=4y2+16x2,
c2=AB2=AP2+BP2=4x2+4y2,
∴a2+b2=20x2+20y2=5(4x2+4y2)=5c2
(3)
解:如图4中,在△AGE和△FGB中,
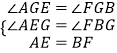 ,
,
∴△AGE≌△FGB,
∴BG=FG,取AB中点H,连接FH并且延长交DA的延长线于P点,
同理可证△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
即PE∥CF,PE=CF,
∴四边形CEPF是平行四边形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)可知AB2+AF2=5BF2,
∵AB=3,BF= ![]() AD=
AD= ![]() ,
,
∴9+AF2=5×( ![]() )2,
)2,
∴AF=4
【解析】(1)解:如图1中,∵CN=AN,CM=BM,
∴MN∥AB,MN= ![]() AB=2
AB=2 ![]() ,
,
∵tan∠PAB=1,
∴∠PAB=∠PBA=∠PNM=∠PMN=45°,
∴PN=PM=2,PB=PA=4,
∴AN=BM= ![]() =2
=2 ![]() .
.
∴b=AC=2AN=4 ![]() ,a=BC=4
,a=BC=4 ![]() .
.
故答案为4 ![]() ,4
,4 ![]() ,
,
如图2中,连接NM,
, ∵CN=AN,CM=BM,
∴MN∥AB,MN= ![]() AB=1,
AB=1,
∵∠PAB=30°,
∴PB=1,PA= ![]() ,
,
在RT△MNP中,∵∠NMP=∠PAB=30°,
∴PN= ![]() ,PM=
,PM= ![]() ,
,
∴AN= ![]() ,BM=
,BM= ![]() ,
,
∴a=BC=2BM= ![]() ,b=AC=2AN=
,b=AC=2AN= ![]() ,
,
故答案分别为 ![]() ,
, ![]() .
.
(1)①首先证明△APB,△PEF都是等腰直角三角形,求出PA、PB、PN、PM,再利用勾股定理即可解决问题.②连接MN,在RT△PAB,RT△PMN中,利用30°性质求出PA、PB、PN、PM,再利用勾股定理即可解决问题.(2)结论a2+b2=5c2 . 设MP=x,NP=y,则AP=2x,BP=2y,利用勾股定理分别求出a2、b2、c2即可解决问题.(3)取AB中点H,连接FH并且延长交DA的延长线于P点,首先证明△ABF是中垂三角形,利用(2)中结论列出方程即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,都是由边长为 1 的正方体叠成的立体图形,例如第⑴个图形由 1 个正方体叠成,第⑵个图形由 4 个正方体叠成,第⑶个图形由 10 个正方体叠成,依次规律,第⑺个图形由( )个正方形叠成.

A. 86 B. 87 C. 85 D. 84
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示,直线y=-
 x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.(1)求出点C的坐标;
(2)若△OQC是等腰直角三角形,则t的值为________;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式: y=
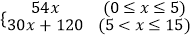 .
.
(1)李明第几天生产的粽子数量为420只?
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本)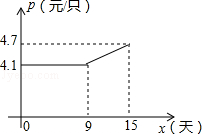
(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2﹣10x+16=0的两个根,且抛物线的对称轴是直线x=﹣2.

(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:(1)△ABD≌△ACD;
(2)BE=CE.

相关试题

