【题目】如下图所示,直线y=-![]() x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标;
(2)若△OQC是等腰直角三角形,则t的值为________;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数表达式.

参考答案:
【答案】(1)点C的坐标为(2,2);(2)t的值为2或4;(3)直线CQ对应的函数表达式为y=-2x+6.
【解析】
(1)以![]() 和
和![]() 组成二元一次方程组,解此方程组即可求得点C的坐标;
组成二元一次方程组,解此方程组即可求得点C的坐标;
(2)由题意可知,∠COQ是锐角,由此可得若△COQ是等腰直角三角形,存在以下两种情况:①∠CQO=90°;②∠OCQ=90°;根据两种情况画出图形,结合已知条件分析解答即可求得对应的t的值;
(3)由题意可知,当点Q是线段OA的中点时,CQ平分△OCA的面积,由此结合已知条件求得点线段OA的中点的坐标即可求得此时CQ的解析式了.
(1)由 解得:
解得:![]() ,
,
∴点C的坐标为(2,2).
(2) 由题意可知,∠COQ是锐角,由此可得若△COQ是等腰直角三角形,存在以下两种情况:①∠CQO=90°;②∠OCQ=90°;先分别解答如下:
I、如图①,当∠CQO=90°,CQ=OQ时,
∵C(2,2),
∴OQ=CQ=2,解得:t=2;

II、如图②,当∠OCQ=90°,OC=CQ时,过点C作CM⊥OA于点M,
∵C(2,2),
∴CM=OM=2,
∴QM=OM=2,
∴OQ=4,
∴t=4.
综上所述,若△OCQ是等腰直角三角形,则t的值为2或4.
(3)令-![]() x+3=0,得x=6,
x+3=0,得x=6,
∴A(6,0).
∴点Q的坐标为(3,0)时,CQ平分△OCA的面积.
设直线CQ的函数表达式为y=kx+b.
把C(2,2),Q(3,0)代入y=kx+b得:
![]() ,
,
解得k=-2,b=6,
∴当直线CQ平分△OCA的面积时,其对应的函数表达式为y=-2x+6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
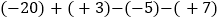 ;(2)
;(2)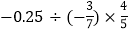 ;
;(3)
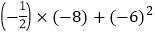 ; (4)
; (4)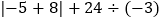 ;
;(5)
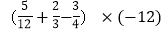 ; (6)
; (6)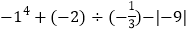 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.

(1)求证:AB是⊙O的切线;
(2)若CF=4,DF= ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,都是由边长为 1 的正方体叠成的立体图形,例如第⑴个图形由 1 个正方体叠成,第⑵个图形由 4 个正方体叠成,第⑶个图形由 10 个正方体叠成,依次规律,第⑺个图形由( )个正方形叠成.

A. 86 B. 87 C. 85 D. 84
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式: y=
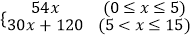 .
.
(1)李明第几天生产的粽子数量为420只?
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本)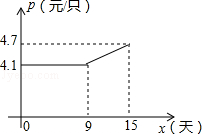
(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元? -
科目: 来源: 题型:
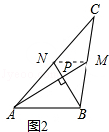
查看答案和解析>>【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.

(1)如图1,当tan∠PAB=1,c=4 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ,AB=3,求AF的长.
,AB=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
相关试题

