【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
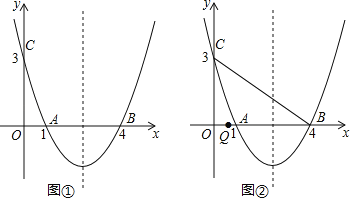
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
参考答案:
【答案】y=![]() x2﹣
x2﹣![]() x+3;在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9;点M的坐标为(
x+3;在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9;点M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)把点A(1,0)、B(4,0)、C(0,3)三点的坐标代入函数解析式,利用待定系数法求解;
(2)A、B关于对称轴对称,连接BC,则BC与对称轴的交点即为所求的点P,此时PA+PC=BC,四边形PAOC的周长最小值为:OC+OA+BC;根据勾股定理求得BC,即可求得;(3)分两种情况分别讨论,即可求得
试题解析:(1)由已知得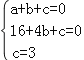 解得
解得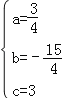 . 所以,抛物线的解析式为y=
. 所以,抛物线的解析式为y=![]() x2﹣
x2﹣![]() x+3.
x+3.
(2)∵A、B关于对称轴对称,如图1,连接BC, ∴BC与对称轴的交点即为所求的点P,此时PA+PC=BC,
∴四边形PAOC的周长最小值为:OC+OA+BC, ∵A(1,0)、B(4,0)、C(0,3),
∴OA=1,OC=3,BC=![]() =5, ∴OC+OA+BC=1+3+5=9;
=5, ∴OC+OA+BC=1+3+5=9;
∴在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9.
(3)∵B(4,0)、C(0,3), ∴直线BC的解析式为y=﹣![]() x+3,
x+3,
①当∠BQM=90°时,如图2,设M(a,b), ∵∠CMQ>90°, ∴只能CM=MQ=b,
∵MQ∥y轴, ∴△MQB∽△COB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得b=
,解得b=![]() ,代入y=﹣
,代入y=﹣![]() x+3得,
x+3得,![]() =﹣
=﹣![]() a+3,解得a=
a+3,解得a=![]() , ∴M(
, ∴M(![]() ,
,![]() );
);
②当∠QMB=90°时,如图3, ∵∠CMQ=90°, ∴只能CM=MQ, 设CM=MQ=m, ∴BM=5﹣m,
∵∠BMQ=∠COB=90°,∠MBQ=∠OBC, ∴△BMQ∽△BOC, ∴![]() =
=![]() ,解得m=
,解得m=![]() ,
,
作MN∥OB, ∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() , ∴MN=
, ∴MN=![]() ,CN=
,CN=![]() , ∴ON=OC﹣CN=3﹣
, ∴ON=OC﹣CN=3﹣![]() =
=![]() , ∴M(
, ∴M(![]() ,
,![]() ),
),
综上,在线段BC上存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形,点M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
①求证:BE=CF;
②若AF=5,BC=6,求△ABC的周长.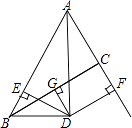
-
科目: 来源: 题型:
查看答案和解析>>【题目】将代数式x2+6x+2化成(x+p)2+q的形式为( )
A. (x-3)2+11 B. (x+3)2-7 C. (x+3)2-11 D. (x+2)2+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】我省为135万名农村中小学生免费提供教科书,减轻了农民的负担135万用科学记数法可表示为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥OD,∠BOC比∠DOC大34°,OE平分∠AOC,求:
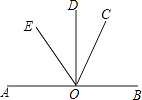
(1)∠COD的大小;
(2)∠DOE的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x﹣3的图象与x轴交点的坐标是 , y轴的交点坐标是 , 顶点坐标是 .
相关试题

