【题目】如图,在平面直角坐标系xOy中,直线y=﹣ ![]() x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.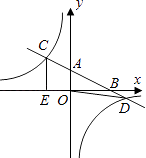
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
(3)x取何值时,反比例函数的值大于一次函数的值.
参考答案:
【答案】
(1)解:∵OE=2,CE⊥x轴于点E.
∴C的横坐标为﹣2,
把x=﹣2代入y=﹣ ![]() x+2得,y=﹣
x+2得,y=﹣ ![]() ×(﹣2)+2=3,
×(﹣2)+2=3,
∴点C的坐标为C(﹣2,3).
设反比例函数的解析式为y= ![]() ,(m≠0)
,(m≠0)
将点C的坐标代入,得3= ![]() .
.
∴m=﹣6.
∴该反比例函数的解析式为y=﹣ ![]() .
.
(2)解:由直线线y=﹣ ![]() x+2可知B(4,0),
x+2可知B(4,0),
解 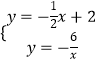 得
得 ![]() ,
, ![]() ,
,
∴D(6,﹣1),
∴S△OBD= ![]() ×4×1=2.
×4×1=2.
(3)由图像可知-2<x<0或x>6
【解析】(1)要求反比例函数的解析式,根据题中的已知条件,CE⊥x轴于点E,OE=2.可知道点C的横坐标为-2,将x=-2代入y=﹣ ![]() x+2可得到点C的纵坐标,用待定系数法可以求出反比例函数的解析式;(2)要求△OBD的面积,就需求出点B和点D的坐标,两函数图像交于点D,建立二元一次方程组,可以求出点D的坐标,直线y=﹣
x+2可得到点C的纵坐标,用待定系数法可以求出反比例函数的解析式;(2)要求△OBD的面积,就需求出点B和点D的坐标,两函数图像交于点D,建立二元一次方程组,可以求出点D的坐标,直线y=﹣ ![]() x+2交x轴于点B,y=0代入即可求得点B的坐标,进而根据三角形的面积公式求得即可。(3)已求出了点D的坐标(6,﹣1),点C的坐标为C(﹣2,3),观察图像可知直线x=-2,y轴,直线x=6将两函数图像分成四个部分,即x<-2,-2<x<0,0<x<6,x>6,观察图像即可得出结论。
x+2交x轴于点B,y=0代入即可求得点B的坐标,进而根据三角形的面积公式求得即可。(3)已求出了点D的坐标(6,﹣1),点C的坐标为C(﹣2,3),观察图像可知直线x=-2,y轴,直线x=6将两函数图像分成四个部分,即x<-2,-2<x<0,0<x<6,x>6,观察图像即可得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)

-
科目: 来源: 题型:
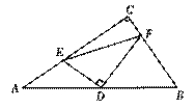
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.
求证:AE2+BF2=EF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解一元一次不等式或不等式组
(1)3(x+2)-8≥1-2(x-1)
(2)
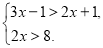
(3)求不等式组
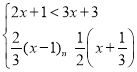 的非负整数解
的非负整数解 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
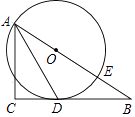
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
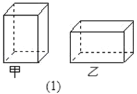
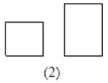
查看答案和解析>>【题目】某纸品加工厂利用边角料裁出正方形和长方形两种硬纸片,长方形的宽与正方形的边长相等(如图2),再将它们制作成甲乙两种无盖的长方体小盒(如图1).现将300张长方形硬纸片和150张正方形硬纸片全部用于制作这两种小盒,可以做成甲乙两种小盒各多少个?(注:图1中向上的一面无盖)
相关试题

