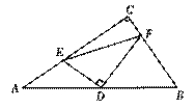
【题目】如图,已知△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.
求证:AE2+BF2=EF2.
参考答案:
【答案】证明见解析
【解析】
过点A作AM∥BC,交FD延长线于点M,连接EM,根据平行线的性质得到∠MAE=∠ACB=90°,∠MAD=∠B,通过“边角边”证明△ADM≌△BDF,则AM=BF,MD=DF,再根据“三线合一”得到EF=EM,在Rt△AEM中利用勾股定理即可得证.
证明:过点A作AM∥BC,交FD延长线于点M,连接EM,
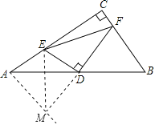
∵AM∥BC,
∴∠MAE=∠ACB=90°,∠MAD=∠B,
∵AD=BD,∠ADM=∠BDF,
∴△ADM≌△BDF(SAS),
∴AM=BF,MD=DF,
又∵DE⊥DF,
∴EF=EM,
∴AE2+BF2=AE2+AM2=EM2=EF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2 .
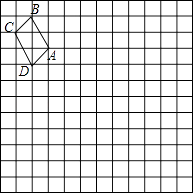
(1)以A为旋转中心,将四边形ABCD顺时针旋转90°,得到四边形AB1C1D1;
(2)以A为位似中心,将四边形ABCD作位似变换,且放大到原来的两倍,得到四边形AB2C2D2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣
 x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.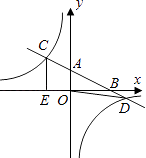
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
(3)x取何值时,反比例函数的值大于一次函数的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解一元一次不等式或不等式组
(1)3(x+2)-8≥1-2(x-1)
(2)
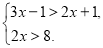
(3)求不等式组
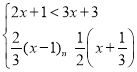 的非负整数解
的非负整数解 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
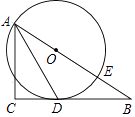
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ,求⊙O的半径.
,求⊙O的半径.
相关试题

